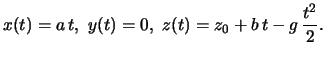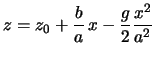

Next: 29-31/10/01. Cap. 6 ,
Up: lezan10102
Previous: 15-17/10/01. Par. 2.1-7, Derivazione
27. Lun. 22 Ott.
Lezione tenuta dalla Dott. Poggiolini: derivata destra e sinistra e punti angolosi.
Esercizi sulle derivate di funzioni definite a tratti
28. Lun. 22 Ott.
Lezione tenuta dalla Dott. Poggiolini: esercizi sulle derivate e la ricerca di rette tangenti.
29. Mar. 23 Ott.
Punti singolari (dove non esiste derivata), critici (dove la derivata e' nulla). Punti interni ed estremi del dominio.
Teorema di Fermat (teorema 2, pg. 157 del testo) con dimostrazione.
Ricerca di massimi e minimi di funzioni. Massimi e minimi locali o relativi.
30. Mar. 23 Ott.
Il teorema del valor medio o di Lagrange e sua interpretazione geometrica e in termini di stima dell'errore.
Esempi:
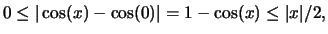 se
se 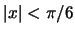 e inoltre esistono
e inoltre esistono 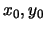 con
con
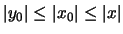 tali che
Riflettere sul fatto che che la seconda disuglianza da' una stima dell'errore migliore della prima se
tali che
Riflettere sul fatto che che la seconda disuglianza da' una stima dell'errore migliore della prima se 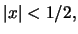 tenere conto che
tenere conto che
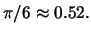 In seguito vedremo che la stima puo' essere ancora migliorata.
In seguito vedremo che la stima puo' essere ancora migliorata.
Esercizio. Verificare che la funzione 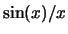 estesa per continuita' a 0 ha derivata 0 in
estesa per continuita' a 0 ha derivata 0 in 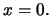 Suggerimento.
Scrivere il rapporto incrementale in 0, poi applicare il teorema di Lagrange a
Suggerimento.
Scrivere il rapporto incrementale in 0, poi applicare il teorema di Lagrange a
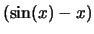 e quindi a
e quindi a
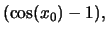 infine passare al limite tenendo conto che
infine passare al limite tenendo conto che
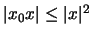
31. Mer. 24 Ott.
Teorema di Rolle e relazione fra gli zeri di 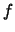 e
e 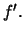 Funzioni con derivata nulla. Primitive (antiderivate, Par.2.9) di una funzione continua su un intervallo ed applicazione allo
studio del problema della caduta dei gravi (Par.3.1): equazioni differenziali, condizioni iniziali, soluzione.
Funzioni con derivata nulla. Primitive (antiderivate, Par.2.9) di una funzione continua su un intervallo ed applicazione allo
studio del problema della caduta dei gravi (Par.3.1): equazioni differenziali, condizioni iniziali, soluzione.
Attenzione: nel testo una primitiva e' chiamata un'antiderivata
Caduta dei gravi.
In un qualsiasi riferimento cartesiano con asse 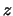 coincidente con la verticale ascendente, se si trascura la resistenza dell'aria,
le equazioni differenziali sono
Scegliendo opportunamente il sistema cartesiano, si puo' sempre ipotizzare che
al tempo 0 il grave si trovi nel punto
coincidente con la verticale ascendente, se si trascura la resistenza dell'aria,
le equazioni differenziali sono
Scegliendo opportunamente il sistema cartesiano, si puo' sempre ipotizzare che
al tempo 0 il grave si trovi nel punto
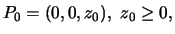 ed abbia velocita'
ed abbia velocita'
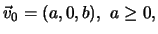 dove
dove
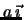 e' la velocita' orizzontale e
e' la velocita' orizzontale e 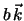 e' la velocita' verticale. Si ottengono le condizioni iniziali
Il teorema di Lagrange ci permette di determinare l'equazione di moto del grave
Si noti che il moto e' verticale se e solo se
e' la velocita' verticale. Si ottengono le condizioni iniziali
Il teorema di Lagrange ci permette di determinare l'equazione di moto del grave
Si noti che il moto e' verticale se e solo se 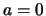 e che se
e che se 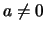 la traiettoria e' una parabola nel piano verticale che contiene
la traiettoria e' una parabola nel piano verticale che contiene
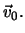 Le equazioni della parabola sono
Esercizio. Si determini l'equazione della traiettoria
Le equazioni della parabola sono
Esercizio. Si determini l'equazione della traiettoria 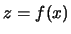 in funzione del modulo (intensita') di
in funzione del modulo (intensita') di 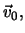 e dell'angolo
(orientato) che la velocita' iniziale forma con il piano orizzontale. Si disegnino i possibili grafici della traiettoria, considerando
che il piano terra abbia quota
e dell'angolo
(orientato) che la velocita' iniziale forma con il piano orizzontale. Si disegnino i possibili grafici della traiettoria, considerando
che il piano terra abbia quota 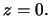 Che significato ha l'approssimazione lineare della traiettoria in
Che significato ha l'approssimazione lineare della traiettoria in 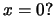
32. Mer. 24 Ott.
Funzioni crescenti e decrescenti su intervalli. Funzioni convesse e concave su intervalli.
Attenzione : sul testo le funzioni convesse vengono chiamate con la concavita' verso l'alto e le funzioni concave con la concavita'
verso il basso
33. Mer. 24 Ott.
Correzione e commenti sul test.


Next: 29-31/10/01. Cap. 6 ,
Up: lezan10102
Previous: 15-17/10/01. Par. 2.1-7, Derivazione
Stefani Gianna
2001-11-06