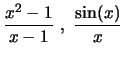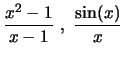

Next: 15-17/10/01. Par. 2.1-7, Derivazione
Up: lezan10102
Previous: 1-3/10/01. Par. 1.1-1.3, 1.5,
13. Lun. 8 Ott.
Lezione tenuta dalla Dott. Poggiolini: esercizi.
14. Lun. 8 Ott.
Lezione tenuta dalla Dott. Poggiolini: esercizi.
15. Mar. 9 Ott.
Funzioni continue in un punto e in un intervallo.
Teorema di permanenza del segno per le funzioni continue.
Esempi di funzioni continue: i polinomi e le funzioni elementari.
Costruzione di funzioni continue: somma, prodotto, quoziente, composizione.
Estensioni continue e discontinuita' rimovibili. Esempi:
Funzioni continue a destra e a sinistra.
Continuita' di funzioni definite a tratti.
Definizione di massimo di una funzione nel suo dominio e su un intervallo.
16. Mar. 9 Ott.
Proprieta' delle funzioni continue sugli intervalli (senza dimostrazione):
i teoremi di Weierstrass (esistenza di massimi e minimi) e dei valori intermedi (radici di equazioni).
Estremi superiore e inferiore di una funzione nel suo dominio e in un intervallo.
Ricerca di soluzioni di equazioni (algoritmo di bisezione) e di immagini di funzioni.
17. Mer. 10 Ott.
Applicazioni delle proprieta' delle funzioni continue:
- segno di un polinomio e di una funzione razionale, es:
- esempi di ricerca grafica di massimi e minimi: cosa si puo' dire dei seguenti problemi con la teoria fin qui svolta?
Massima (minima) area dato il perimetro
 di un rettangolo non degenere
Minimo (massimo) perimetro data l'area
di un rettangolo non degenere
Minimo (massimo) perimetro data l'area  di un rettangolo
di un rettangolo
18. Mer.10 Ott.
Lezioni al computer su limiti, funzioni continue, esistenza di massimi e minimi.
19. Mer. 10 Ott.
Incrementi e distanze nel piano. Vettori. Rapporto incrementale di una funzione in un punto e suo significato geometrico.
Riflettere sulla seguente affermazione:
una funzione e' continua se e solo se
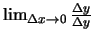 e' una forma indeterminata.
Definizione di derivata in un punto.
e' una forma indeterminata.
Definizione di derivata in un punto.


Next: 15-17/10/01. Par. 2.1-7, Derivazione
Up: lezan10102
Previous: 1-3/10/01. Par. 1.1-1.3, 1.5,
Stefani Gianna
2001-11-06