


Next: Calcolo della soluzione
Up: No Title
Previous: No Title
Teorema 1.1
Sia
![$f:[a,b]\rightarrow \R$](img1.gif)
continua e sia
f(
a)
f(
b)<0, allora esiste
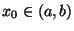
tale che
f(
x0)=0.
Per fissare le idee faremo la dimostrazione nel caso
lo studente ripeta la dimostrazione nel caso
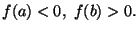
La dimostrazione si propone di "costruire " la soluzione come l'unico punto
comune a una successione di intervalli contenuti uno nell'altro.
Il procedimento é basato sulla seguente procedura di iterazione,
detta algoritmo di bisezione,
che permette di costruire, a partire da un intervallo che soddisfi
le ipotesi del teorema, un sottointervallo di lunghezza metá che soddisfa ancora
alle ipotesi del teorema.
Iterazione. Sia
![$I=[\alpha,\beta]$](img5.gif) un intervallo che soddisfa alle ipotesi
del teorema e sia
un intervallo che soddisfa alle ipotesi
del teorema e sia
 il
suo punto medio, scegliamo un nuovo intervallo J in base al
valore di f(m)
il
suo punto medio, scegliamo un nuovo intervallo J in base al
valore di f(m)
La procedura di iterazione ci permette di generare una successione decrescente
di intervalli nel modo seguente.
-
Partiamo dall'intervallo
I=I0=[a,b] e generiamo un nuovo intervallo
I1=[a1,b1] secondo la procedura di iterazione.
-
Se non abbiamo trovato la soluzione, ripetiamo la procedura per
trovare
I2=[a2, b2] a partire da I1.
-
Procedendo in maniera analoga, se l'algoritmo non
si arresta, costruiamo una successione decrescente di intervalli
di lunghezza data da
La successione 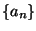 e' crescente e superiormente limitata (ogni bne' una limitazione superiore), analogamente
la successione
e' crescente e superiormente limitata (ogni bne' una limitazione superiore), analogamente
la successione 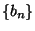 e' decrescente e inferiormente limitata.
Posto
e' decrescente e inferiormente limitata.
Posto
otteniamo che
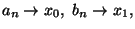 ma
ma
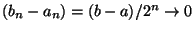 e quindi dalle proprietá dei limiti segue che
e quindi dalle proprietá dei limiti segue che
x0 =x1.
Individuato x0 come candidato, dobbiamo dimostrare che é
effettivamente una soluzione dell'equazione. In questo interviene in maniera essenziale
l'ipotesi di continuitá di f attraverso il teorema
della permanenza del segno. Infatti, per la procedura che abbiamo seguito,
in ogni delta-intorno di x0 ci
sono sia punti an su cui la funzione é positiva, sia punti
bn su cui la funzione é negativa, quindi l'unica
possibilitá di non contraddire il teorema della permanenza del segno
é che sia
f(x0)=0.



Next: Calcolo della soluzione
Up: No Title
Previous: No Title
1999-10-12
![\begin{displaymath}\begin{array}{lll}
\text{se} &f(m)=0 &\text{abbiamo trovato l...
...ext{se} &f(m)<0 &\text{si pone} \quad J=[\alpha,m].
\end{array}\end{displaymath}](img7.gif)