


Next: Seconda settimana
Up: No Title
Previous: No Title
1. Lun. 21 Set.
Indicazioni sul corso. Prerequisiti: elementi teoria degli insiemi,
piano cartesiano ed equazioni della retta, espressioni algebriche,
funzioni trigonometriche di un angolo e relazioni, triangolo rettangolo,
formule di addizione e prostaferesi (da ricavare dalle precedenti).
2. Lun. 21 Set.
Proprieta' algebriche dei numeri reali.
 Dimostrazione di: Radice di 2 non e' razionale.
Implicazioni e dimostrazione per assurdo (senza formalizzare, con
esempi).
Dimostrazione di: Radice di 2 non e' razionale.
Implicazioni e dimostrazione per assurdo (senza formalizzare, con
esempi).
3. Mar. 22 Set.
Relazione d'ordine.
 Esempi :
Esempi :
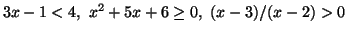 Dimostrazione di: l'unico numero reale nonnegativo minore di ogni
numero positivo è 0. Introduzione dei quantificatori
Dimostrazione di: l'unico numero reale nonnegativo minore di ogni
numero positivo è 0. Introduzione dei quantificatori
 e loro negazione (senza formalizzare, con esempi).
e loro negazione (senza formalizzare, con esempi).
4. Mar. 22 Set.
Valore assoluto e proprietà. Per
 uguaglianza fra
uguaglianza fra
 e
e
 Intervalli (limitati) e semirette
(intervalli illimitati).
Intervalli (limitati) e semirette
(intervalli illimitati).
5. Mer. 23 Set.
Distanza, intorni, punto medio. Max e min di un insieme. Insiemi limitati,
limitazioni.
Estremo inferiore e superiore.
6. Mer. 23 Set.
Lezione non tenuta
7. Gio. 24 Set.
Lezione tenuta dal Prof. Canarutto: polinomi, radici e molteplicita'
divisione
8. Gio. 24 Set.
Lezione tenuta dal Prof. Canarutto: decomposizione dei polinomi,
esercizio.
9. Ven. 25 Set.
Lezione tenuta dal Prof. Canarutto: esercizi su equazioni e disequazioni
razionali.
10. Ven. 25 Set.
Lezione tenuta dal Prof. Canarutto: esercizi su equazioni e disequazioni
con valore assoluto.



Next: Seconda settimana
Up: No Title
Previous: No Title
Gianna Stefani
1998-12-14