

Next: Quinta settimana
Up: lez0001bis
Previous: lez0001bis
33. Lun. 30 Ott.
Lezione tenuta dal Dott. Mugelli: Esercizi su convergenza di serie e funzioni.
34. Lun. 30 Ott.
Lezione tenuta dal Dott. Mugelli: Esercizi domini di funzioni.
35. Lun. 30 Ott.
Lezione tenuta dal Dott. Mugelli: Esercizi su differenziabilita',
derivate parziali e piano tangente al grafico.
36. Mar. 31 Ott.
Per semplicita' tutte le funzioni saranno 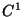 in un intorno dei punti
considerati.
Possibili notazioni
in un intorno dei punti
considerati.
Possibili notazioni
con 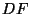 si identificano la matrice Jacobiana e l'applicazione lineare associata.
si identificano la matrice Jacobiana e l'applicazione lineare associata.
La matrice Jacobiana nel caso di curve e funzioni a valori in 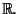 Derivate parziali e matrice Jacobiana della composizione, idea della
dimostrazione
Derivate parziali e matrice Jacobiana della composizione, idea della
dimostrazione
Esempio:
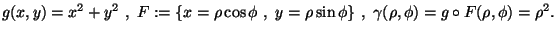
Composizione con le curve e derivate direzionali, il simbolo
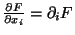 .
Curve coordinate per le coordinate polari nel piano e curve
e superfici
coordinate le coordinate cilindriche (per esercizio).
.
Curve coordinate per le coordinate polari nel piano e curve
e superfici
coordinate le coordinate cilindriche (per esercizio).
37. Mar. 31 Ott.
Esercizio proposto: calcolare in piu' maniere il vettore tangente a
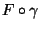 nel punto
nel punto
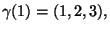 se
se
Coordinate polari nello spazio, formule, curve e superfici coordinate,
matrice Jacobiana
38. Gio. 2 Nov.
Funzione inversa e differenziabilita'
Cambiamento di coordinate inverso
per le coordinate polari nel piano e nello spazio.
39. Gio. 2 Nov.
Curve regolari cioe'
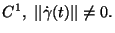 Esempio:
Esempio:
la prima non e' regolare in 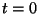 la seconda e' regolare, localmente
invertibile ma non invertibile (ha un "nodo" nell'origine).
Retta tangente ad una curva regolare (Bacciotti-Ricci
cap.III n.1)
Cenni sulle superfici regolari
la seconda e' regolare, localmente
invertibile ma non invertibile (ha un "nodo" nell'origine).
Retta tangente ad una curva regolare (Bacciotti-Ricci
cap.III n.1)
Cenni sulle superfici regolari
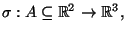 cioe'
cioe' 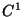 e con rango della matrice Jacobiana uguale a 2, condizioni
geometriche equivalenti. Piano tangente ad una superficie regolare. Esempi:
le superfici coordinate delle coordinate polari.
(Bacciotti-Ricci capIII n.5 escluso il cambiamento di coordinate e seguenti).
e con rango della matrice Jacobiana uguale a 2, condizioni
geometriche equivalenti. Piano tangente ad una superficie regolare. Esempi:
le superfici coordinate delle coordinate polari.
(Bacciotti-Ricci capIII n.5 escluso il cambiamento di coordinate e seguenti).
40. Ven. 3 Nov.
Derivate di ordine superiore, teorema di Schwartz (senza dimostrazione).
Matrice Hessiana,
esempio:
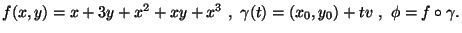
41. Ven. 3 Nov.
Formula di Taylor al secondo ordine (senza dimostrazione),
analogia con il
caso di una variabile. Massimi e minimi locali, punti stazionari (singolari).
42. Ven. 3 Nov.
Condizione necessarie e condizioni sufficienti per minimi e massimi locali.


Next: Quinta settimana
Up: lez0001bis
Previous: lez0001bis
Stefani Gianna
2000-11-20