

Next: About this document ...
Up: lez0001
Previous: Seconda settimana
23. Lun. 23 Ott.
Lezione tenuta dal Dott. Mugelli: Esercizi su limiti, domini e continuita'.
24. Lun. 23 Ott.
Lezione tenuta dal Dott. Mugelli: Esercizi su limiti, domini e continuita'.
25. Lun. 23 Ott.
Lezione tenuta dal Dott. Mugelli: Esercizi su limiti, domini e continuita'.
26. Mar. 24 Ott.
Estensioni del concetto di derivata. Vettore tangente ad (al supporto di)
una curva, es. equazioni parametriche di una circonferenza.
Differenziale di una funzione
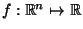 , funzioni lineari. Differenziabilita' e continuita'.
, funzioni lineari. Differenziabilita' e continuita'.
27. Mar. 24 Ott.
Derivate parziali e direzionali e loro interpretazione come derivata di una
funzione composta.
Condizione sufficiente di differenziabilita': funzioni 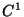 in un intorno, cioe'
derivate parziali continue in un intorno
(senza dimostrazione). L'esistenza delle derivate parziali e direzionali
non implica la continuita' e quindi la differenziabilita', esempio:
in un intorno, cioe'
derivate parziali continue in un intorno
(senza dimostrazione). L'esistenza delle derivate parziali e direzionali
non implica la continuita' e quindi la differenziabilita', esempio:
Esercizio proposto: determinare i punti in cui le seguenti funzioni sono continue,
differenziabili ed ammettono derivate parziali e direzionali.
29. Gio. 26 Ott.
Differenziale e gradiente di una funzione e loro
relazione con le derivate direzionali. Derivata della composizione di una
funzione con una curva. Piano tangente al grafico
di una funzione come grafico della sua approssimazione
lineare. Direzione di massima pendenza.
Esempio:
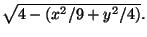
Esercizi proposti:
1) Interpretare il grafico di una funzione di una variabile
come sostegno di una curva e discutere la relazione
fra il concetto di retta tangente al grafico e vettore tangente alla curva.
2) Calcolare (dopo aver verificato in quali punti e' differenziabile)
il gradiente di
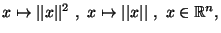 darne una interpretazione geometrica e
verificarne il risultato per
darne una interpretazione geometrica e
verificarne il risultato per 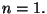
28. Gio. 26 Ott.
Applicazione della derivata della composizione fra curve e funzioni:
1) Energia di una particella in un campo di forze conservative.
Se indichiamo con
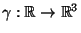 il moto di una particella
in un campo di forze
il moto di una particella
in un campo di forze
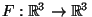 dato da
dato da 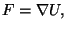
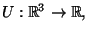 abbiamo
conservazione dell'energia
abbiamo
conservazione dell'energia
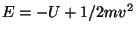 (
(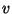 e' la velocita' scalare della particella)
, lungo la traiettoria. Abbiamo cioe'
e' la velocita' scalare della particella)
, lungo la traiettoria. Abbiamo cioe'
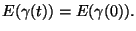 Per verificarlo basta derivare
Per verificarlo basta derivare
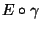 , tenendo
conto che
, tenendo
conto che
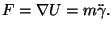
30. Ven. 27 Ott.
Angolo fra piano tangente al grafico e verticale, retta tangente alle curve di
livello. Applicazione della derivata della composizione fra curve e funzioni:
1) Dimostrare che se una funzione ha derivate parziali nulle su
un aperto convesso (connesso)
allora e' costante. (Usare il teorema di Lagrange)
1a) Es. n. 3.68a di Marcellini-Sbordone: discutere l'identita'
31. Ven. 27 Ott.
2) Dimostrare che se una funzione e' 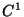 su un convesso compatto
su un convesso compatto 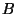 ,
allora esiste una costante
,
allora esiste una costante
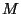 tale che
tale che
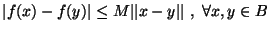 . (usare il teorema di
Lagrange)
. (usare il teorema di
Lagrange)
32. Ven. 27 Ott.
Funzioni
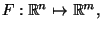 differenziabilita', matrice Jacobiana,
condizione sufficiente di differenziabilita'. Matrice Jacobiana del cambiamento
di coordinate polari nel piano. Esercizio proposto: rivedere i prodotti
righe per colonne fra matrici e tutte le proprieta' delle matrici.
differenziabilita', matrice Jacobiana,
condizione sufficiente di differenziabilita'. Matrice Jacobiana del cambiamento
di coordinate polari nel piano. Esercizio proposto: rivedere i prodotti
righe per colonne fra matrici e tutte le proprieta' delle matrici.


Next: About this document ...
Up: lez0001
Previous: Seconda settimana
Stefani Gianna
2000-10-27