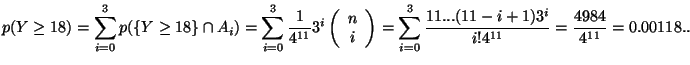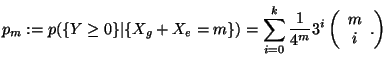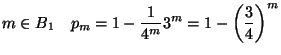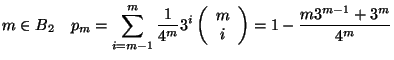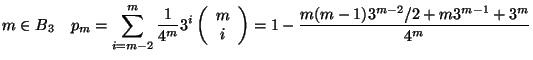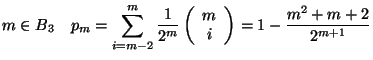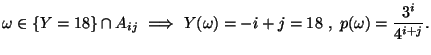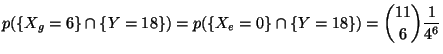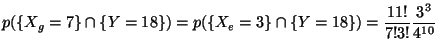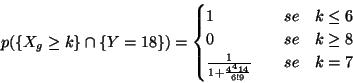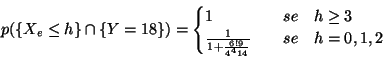

Next: About this document ...
Up: ese20di
Previous: Esercizio
Il problema puo' essere schematizzato pensando ad 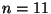 copie
indipendenti
dello spazio di probabilita' formato da una domanda.
Poiche' non dare risposta contribuisce solo a
determinare il numero di domande che entrano effettivamente
in "gioco",
i possibili esiti
(risposte)
copie
indipendenti
dello spazio di probabilita' formato da una domanda.
Poiche' non dare risposta contribuisce solo a
determinare il numero di domande che entrano effettivamente
in "gioco",
i possibili esiti
(risposte) 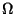 possono essere schematizzati con
possono essere schematizzati con
g=risposta giusta con probabilita' 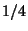
e=risposta errata con probabilita' 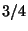
*=nessuna risposta con probabilita' 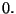
Il punteggio di ciascuna domanda puo' essere visto
come la variabile
aleatoria
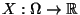 definita da
definita da
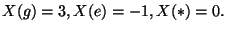 Definendo per
Definendo per
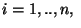 si ottiene il punteggio globale come somma di variabili
aleatorie indipendenti
si ottiene il punteggio globale come somma di variabili
aleatorie indipendenti
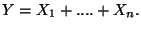
Si possono anche introdurre le variabili aleatorie
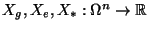 come quelle che contano
il numero di
risposte giuste, errate e non date rispettivamente.
come quelle che contano
il numero di
risposte giuste, errate e non date rispettivamente.
Domanda 1
Calcolare il valore atteso del punteggio su ogni domanda e globale.
Soluzione
![$ E[X]=3/4(-1)+3/4=0,$](img19.gif) quindi
quindi
![$ E[Y]=n.0=0.$](img20.gif) Il "gioco" e' equo.
Il "gioco" e' equo.
Riflettere su quali altri punteggi si possono dare se si
vuole far rimanere il valore atteso di 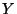 uguale a
uguale a 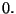
Domanda 2
Calcolare la probabilita' di avere un punteggio di almeno 18
scegliendo tutte le risposte a caso.
Soluzione
In questo caso si ipotizza di dare tutte le risposte, quindi lo spazio di probabilita'
puo' essere visto come una distribuzione binomiale 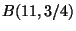 (considerando
e=successo!!) e
si deve calcolare
Si puo' definire una partizione di
(considerando
e=successo!!) e
si deve calcolare
Si puo' definire una partizione di 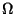 con
se
con
se
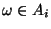 allora
allora
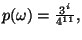 e
D'altra parte la cardinalita' di
e
D'altra parte la cardinalita' di 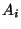 e' data da
e' data da
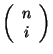 e quindi
e quindi
Domanda 3
Calcolare la probabilita' di aumentare il punteggio dando a caso
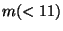
risposte. Studiare la probabilita' in funzione di
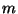
.
Soluzione
Si deve calcolare la probabilita' condizionata
Si puo' ragionare in maniera analoga al punto precedente sostituendo
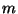 a
a 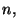 oppure in maniera equivalente definendo
oppure in maniera equivalente definendo
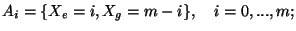 in ogni caso
se
in ogni caso
se
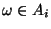 allora
allora
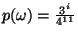 e
Se si indica
e
Se si indica 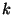 il piu' grande intero minore di
il piu' grande intero minore di 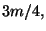 otteniamo
In particolare avremo
Per studiare
otteniamo
In particolare avremo
Per studiare 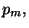 conviene studiare il complementare, infatti si
vede subito che gli esiti che danno un punteggio negativo sono
in numero minore di quelli che danno un esito positivo.
conviene studiare il complementare, infatti si
vede subito che gli esiti che danno un punteggio negativo sono
in numero minore di quelli che danno un esito positivo.
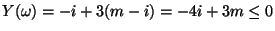 implica
implica
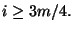 Se si indica
Se si indica 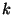 il piu' piccolo intero minore o uguale a
il piu' piccolo intero minore o uguale a 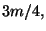 otteniamo
otteniamo
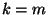 se
se
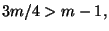 inoltre
inoltre 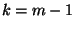 se
se
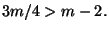 Procedendo in maniera analoga
otteniamo
Procedendo in maniera analoga
otteniamo
per l'ultima limitazione si ricordi che si richiede 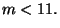 Ponendo
abbiamo
Ponendo
abbiamo
Si vede quindi che
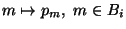 e'
crescente, mentre
e'
crescente, mentre
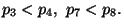
Il grafico e' dato da
Disegnarlo in un sistema di assi cartesiani.
Domanda 4
Nel caso che per una domanda si sia certi che la risposta giusta
sia da scegliere
fra due, che probabilita' si ha di aumentare il punteggio
scegliendola a caso fra quelle due?
Soluzione
La probabilita' e' ovviamente 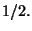
Domanda 5
Nel caso che per
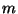
domande si sia certi che la risposta giusta
sia da scegliere
fra due, che probabilita' si ha di aumentare il
punteggio scegliendola per ognuna delle
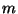
domande a caso?
Studiare tale probabilita' in funzione di
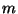
.
Soluzione
L'esercizio e' simile al n.3, cambia solo la probabilita' da attribuire
alle risposte. Pertanto con le stesse notazioni avremo:
Si vede quindi che
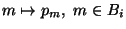 e'
crescente, mentre
e'
crescente, mentre
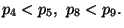
Disegnare il grafico.
Domanda 6
Se il punteggio di un test e'
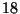
che probabilita' si
ha di aver dato almeno
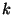
risposte giuste? E al piu'
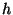
risposte sbagliate?
Studiare le probabilita' in funzione
di
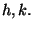
Soluzione
Si tratta di calcolare le due probabilita' condizionate
Ponendo
abbiamo che
D'altra parte
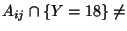 se esolo se
se esolo se
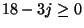 e
e
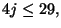 quindi per la coppia
quindi per la coppia 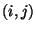 abbiamo solo le possibilita'
Avremo
abbiamo solo le possibilita'
Avremo
Le probabilita' richieste valgono
Domanda 7
Ripetere il precedente esercizio per diversi punteggi del test, ad esempio
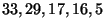
Soluzione
Ripetendo il ragionamento precedente si vede che per
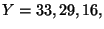 si hanno le sole possibilita'
rispettivamente e
le probabilita' possono valere solo
si hanno le sole possibilita'
rispettivamente e
le probabilita' possono valere solo 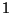 o
o 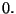
Per 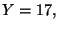 le possibilita' sono
Per
le possibilita' sono
Per 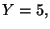 le possibilita' sono
le possibilita' sono


Next: About this document ...
Up: ese20di
Previous: Esercizio
Stefani Gianna
2000-12-30
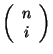 e quindi
e quindi