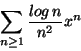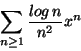Sessione autunnale, secondo appello

Analisi Matematica I (Prof. Stefani) Prova scritta del 2/10/1998 A
Durata: ore 2

Cognome, nome, matricola

 
 
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte senza giustificazione non verranno ritenute valide. Ove richiesto la risposta deve essere riportata sul presente foglio.
 
ES.1 (p.nti 6) a) Determinare per quali valori di 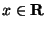$x\in {\bf R}$ la seguente serie converge

$$\sum_{n\geq 1}\frac{log\,n}{n^2}x^n$$

Risposta
...
ES.2 (p.nti 6)

$$\mbox{Definiamo} \hspace*{5cm} f(x)=(x^2-x^4)^\pi .\hspace*{5cm}$$

a) Determinare il dominio di f
Risposta
...
b) Giustificare l'affermazione f ha massimo e minimo assoluti
...
c) Determinare il max e min assoluto ed i punti dove vengono raggiunti
Risposta
......
ES.3 (p.nti 6)
a) Determinare il polinomio di Taylor di grado 4 in 0della funzione

f(x)=e^x+2x2-x-5x²/4

Risposta
...
b) Posso decidere se f(0) e' massimo o minimo relativo per la funzione usando la risposta al punto a)? In caso affermativo indicare cosa sia.
Risposta
...
ES.4 (p.nti 6 ) Determinare numero e segno delle soluzioni della seguente equazione

$$\frac{6x^5-9x^4+2x^3-1}{2x-1}=0$$

Si consiglia di non usare metodi algebrici
Risposta
...
ES.5 (p.nti 6 ) Determinare per quali valori di 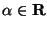$\alpha\in {\bf R}$converge il seguente integrale improprio

$$\int_0^{+\infty} \frac{e^{-x}}{\sqrt{(x+1)^\alpha}}dx$$

Risposta
...

Analisi Matematica I (Prof. Stefani) Prova scritta del 2/10/1998 B
Durata: ore 2

Cognome, nome, matricola

 
 
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte senza giustificazione non verranno ritenute valide. Ove richiesto la risposta deve essere riportata sul presente foglio.
 
ES.1 (p.nti 6) a) Determinare per quali valori di 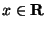$x\in {\bf R}$ la seguente serie converge

$$\sum_{n\geq 1}x^nsen(1/n)$$

Risposta
...
ES.2 (p.nti 6)

$$\mbox{Definiamo} \hspace*{5cm} f(x)=(x^3-2x^4)^e .\hspace*{5cm}$$

a) Determinare il dominio di f
Risposta
...
b) Giustificare l'affermazione f ha massimo e minimo assoluti
...
c) Determinare il max e min assoluto ed i punti dove vengono raggiunti
Risposta
......
ES.3 (p.nti 6)
a) Determinare il polinomio di Taylor di grado 4 in 0della funzione

f(x)=sen(x+2x²)-x

Risposta
...
b) Posso decidere se f(0) e' massimo o minimo relativo per la funzione usando la risposta al punto a)? In caso affermativo indicare cosa sia.
Risposta
...
ES.4 (p.nti 6 ) Determinare numero e segno delle soluzioni della seguente equazione

2x+3+log|x|=0

Si consiglia di non usare metodi algebrici
Risposta
...
ES.5 (p.nti 6 ) Determinare per quali valori di 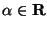$\alpha\in {\bf R}$converge il seguente integrale improprio

$$\int_0^{+\infty} \frac{log(1+1/x)}{\sqrt[3]{(x^2+1)^\alpha}}dx$$

Risposta
...

Analisi Matematica I (Prof. Stefani) Prova scritta del 2/10/1998 C
Durata: ore 2

Cognome, nome, matricola

 
 
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte senza giustificazione non verranno ritenute valide. Ove richiesto la risposta deve essere riportata sul presente foglio.
 
ES.1 (p.nti 6) a) Determinare per quali valori di 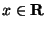$x\in {\bf R}$ la seguente serie converge

$$\sum_{n\geq 1}e^{n\,log\,n}x^n$$

Risposta
...
ES.2 (p.nti 6)

$$\mbox{Definiamo} \hspace*{5cm} f(x)=(2x^3-x^6)^{\sqrt 2} .\hspace*{5cm}$$

a) Determinare il dominio di f
Risposta
...
b) Giustificare l'affermazione f ha massimo e minimo assoluti
...
c) Determinare il max e min assoluto ed i punti dove vengono raggiunti
Risposta
......
ES.3 (p.nti 6)
a) Determinare il polinomio di Taylor di grado 4 in 0della funzione

$$f(x)=cos(x+2x^2)+x^2/2+2x^3+47\,x^4/24$$

Risposta
...
b) Posso decidere se f(0) e' massimo o minimo relativo per la funzione usando la risposta al punto a)? In caso affermativo indicare cosa sia.
Risposta
...
ES.4 (p.nti 6 ) Determinare numero e segno delle soluzioni della seguente equazione

x²+100+log|x+2|=0

Si consiglia di non usare metodi algebrici
Risposta
...
ES.5 (p.nti 6 ) Determinare per quali valori di 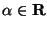$\alpha\in {\bf R}$converge il seguente integrale improprio

$$\int_0^{+\infty} \frac{sen(1/x)}{\sqrt{(x^3+2)^\alpha}}dx$$

Risposta
...

Analisi Matematica I (Prof. Stefani) Prova scritta del 2/10/1998 D
Durata: ore 2

Cognome, nome, matricola

 
 
Rispondere ai seguenti quesiti, giustificando in fogli separati le risposte. Risposte senza giustificazione non verranno ritenute valide. Ove richiesto la risposta deve essere riportata sul presente foglio.
 
ES.1 (p.nti 6) a) Determinare per quali valori di 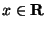$x\in {\bf R}$ la seguente serie converge

$$\sum_{n\geq 1}e^{\frac{log\,n}{n}}x^n$$

Risposta
...
ES.2 (p.nti 6)

$$\mbox{Definiamo} \hspace*{5cm} f(x)=(3\,x^2-2\,x^6)^{\sqrt 3} .\hspace*{5cm}$$

a) Determinare il dominio di f
Risposta
...
b) Giustificare l'affermazione f ha massimo e minimo assoluti
...
c) Determinare il max e min assoluto ed i punti dove vengono raggiunti
Risposta
......
ES.3 (p.nti 6)
a) Determinare il polinomio di Taylor di grado 4 in 0della funzione

$$f(x)=log(1+x+2\,x^2)-x-2\,x^2$$

Risposta
...
b) Posso decidere se f(0) e' massimo o minimo relativo per la funzione usando la risposta al punto a)? In caso affermativo indicare cosa sia.
Risposta
...
ES.4 (p.nti 6 ) Determinare numero e segno delle soluzioni della seguente equazione

$$\frac{2\,x^6-3\,x^4-1}{x-1}=0$$

Si consiglia di non usare metodi algebrici
Risposta
...
ES.5 (p.nti 6 ) Determinare per quali valori di 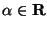$\alpha\in {\bf R}$converge il seguente integrale improprio

$$\int_0^{+\infty} \frac{cos(1/x)-1}{\sqrt[5]{(x^6+x)^\alpha}}dx$$

Risposta
...