


Next: About this document ...
Up: Appendice
Previous: Misura e integrazione astratta
1. Teorema di esistenza della misura di Lebesgue in 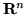 . Esiste
una misura positiva completa
. Esiste
una misura positiva completa 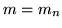 definita su una
definita su una 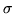 -algebra
-algebra 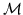 in
in
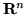 , che ha le seguenti proprietà:
, che ha le seguenti proprietà:
i)
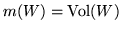 per ogni iperrettangolo di
per ogni iperrettangolo di 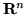 .
.
ii) 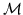 contiene i boreliani e
contiene i boreliani e 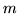 è regolare.
è regolare.
iii) 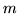 è invariante per traslazione, cioè
è invariante per traslazione, cioè 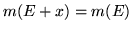 per ogni
per ogni
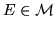 e per ogni
e per ogni
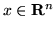 .
.
iv) (Unicità di 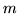 ). Se
). Se 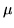 è una qualsiasi misura di Borel in
è una qualsiasi misura di Borel in
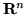 invariante per traslazione e a valori finiti sui compatti, allora
esiste una costante
invariante per traslazione e a valori finiti sui compatti, allora
esiste una costante 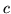 tale che
tale che
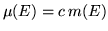 per ogni boreliano
per ogni boreliano
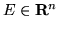 .
.
2. Si dice che
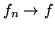 in misura se, per ogni fissato
in misura se, per ogni fissato 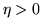 ,
,
Si ha che:
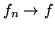 q.o.
q.o.
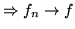 in misura.
in misura.
3. Le funzioni monotone (e quindi anche le differenze di monotone) sono derivabili
q.o.
4. Una funzione  si dice assolutamente continua (a.c.) se: per ogni
si dice assolutamente continua (a.c.) se: per ogni 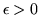 esiste
esiste 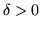 tale che, comunque si scelga un numero finito di intervalli
tale che, comunque si scelga un numero finito di intervalli
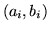 non coprentisi e con
non coprentisi e con
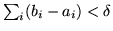 , si abbia
, si abbia
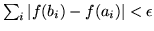 . Le funzioni lipschitziane sono a.c. Le funzioni a.c.
sono derivabili q.o.
. Le funzioni lipschitziane sono a.c. Le funzioni a.c.
sono derivabili q.o.
5. Se 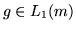 , posto, per ogni
, posto, per ogni 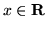 ,
,
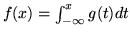 , allora
, allora  è a.c. e inoltre
è a.c. e inoltre 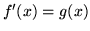 q.o.
q.o.
6. Per le funzioni a.c. vale la formula fondamentale del calcolo integrale (per
l'integrale di Lebesgue). Precisamente vale il seguente fatto. Condizione necessaria
e sufficiente a che la formula
valga per tutti gli 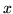 di un intervallo
di un intervallo ![$[a,b]$](img1083.gif) , è che
, è che  sia a.c. su
sia a.c. su ![$[a,b]$](img1083.gif) .
.
7. Teorema di Fubini in 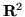 . Sia
. Sia
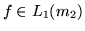 . Allora
. Allora
i) per quasi tutti gli 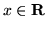 la funzione
la funzione
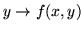 appartiene a
appartiene a
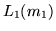 ;
;
ii) la funzione
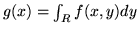 appartiene a
appartiene a 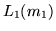 ;
;
iii) risulta
Analogamente per quasi tutti gli 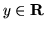 , esiste l'integrale
, esiste l'integrale
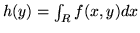 , e si ha
, e si ha



Next: About this document ...
Up: Appendice
Previous: Misura e integrazione astratta
Stefani Gianna
2000-11-06