


Next: Misura di Lebesgue
Up: Appendice
Previous: Appendice
1. Uno spazio di misura è una terna
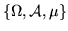 dove
dove 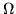 è un insieme, A una
è un insieme, A una 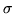 -algebra di
-algebra di
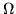 e
e 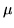 una misura positiva su A (
una misura positiva su A (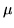 soddisfa gli stessi
assiomi di una probabilità
soddisfa gli stessi
assiomi di una probabilità 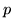 salvo che non si chiede che
salvo che non si chiede che
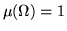 ,
inoltre è permesso il valore +
,
inoltre è permesso il valore +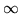 ). Gli elementi della
). Gli elementi della 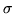 -algebra
-algebra
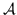 sono i sottoinsiemi misurabili di
sono i sottoinsiemi misurabili di 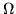 .
.
2. Una
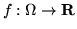 si dice misurabile se
si dice misurabile se 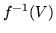 è
misurabile (cioè appartiene ad
è
misurabile (cioè appartiene ad 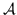 ) per ogni aperto
) per ogni aperto 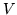 di
di 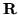 .
.
3. Indicheremo con 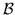 la
la 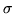 -algebra generata dagli aperti di
-algebra generata dagli aperti di
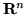 , i suoi elementi vengono chiamati boreliani. Una funzione
, i suoi elementi vengono chiamati boreliani. Una funzione
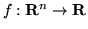 si dice Borel misurabile se è
misurabile quando in
si dice Borel misurabile se è
misurabile quando in 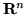 ci sia la
ci sia la 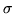 -algebra dei boreliani. Ogni
-algebra dei boreliani. Ogni  continua risulta dunque Borel misurabile.
continua risulta dunque Borel misurabile.
4. In generale se
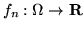 sono misurabili, tali risultano
anche le funzioni
sono misurabili, tali risultano
anche le funzioni
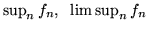 ,
in particolare, se esiste, è misurabile
,
in particolare, se esiste, è misurabile
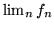 .
.
5. Sia
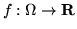 , definiamo
, definiamo
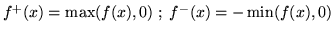 , allora
, allora 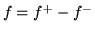 porge una decomposizione canonica
di una funzione nella differenza di due funzioni positive. Per quanto detto se
porge una decomposizione canonica
di una funzione nella differenza di due funzioni positive. Per quanto detto se  è misurabile, tali sono anche
è misurabile, tali sono anche 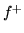 e
e 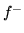 .
.
6. Una funzione 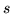 su
su 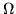 che prende solo un numero finito di valori
(positivi) è detta semplice. Se
che prende solo un numero finito di valori
(positivi) è detta semplice. Se 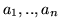 sono i valori assunti da
sono i valori assunti da 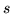 ,
allora
,
allora
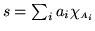 , dove
, dove
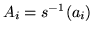 e
e
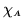 indica la funzione
caratteristica di
indica la funzione
caratteristica di 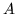 . Chiaramente
. Chiaramente 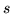 è misurabile se e solo se
è misurabile ogni insieme
è misurabile se e solo se
è misurabile ogni insieme 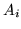 .
.
7. Sia
![$f: \Omega \rightarrow [0, +\infty]$](img1037.gif) misurabile. Esiste una successione di
funzioni semplici
misurabile. Esiste una successione di
funzioni semplici 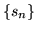 tale che
tale che
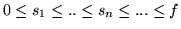 ;
;
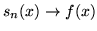 per ogni
per ogni 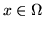 . Inoltre se
. Inoltre se  è limitata la
convergenza è uniforme.
è limitata la
convergenza è uniforme.
8. Sia 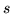 una funzione semplice (misurabile),
una funzione semplice (misurabile),
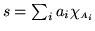 ,
,
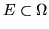 misurabile,
l'integrale (di Lebesgue) di
misurabile,
l'integrale (di Lebesgue) di 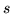 su
su 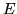 è definito da
è definito da
Sia  una funzione positiva misurabile, l'integrale di
una funzione positiva misurabile, l'integrale di  su
su
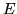 è definito da
è definito da
9. Teorema della convergenza monotona: sia
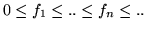 ,
siano le
,
siano le 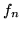 misurabili e
misurabili e
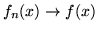 per ogni
per ogni 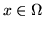 ,
allora (
,
allora ( è misurabile e)
è misurabile e)
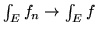 .
.
10. 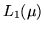 è lo spazio delle funzioni
è lo spazio delle funzioni 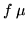 -misurabili su
-misurabili su 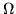 e tali
che
e tali
che
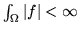 . Se
. Se
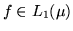 , l'integrale di
, l'integrale di  su
su
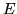 è definito da
è definito da
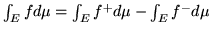 ;
poichè
;
poichè
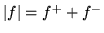 si ha
si ha
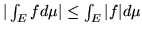 .
.
11. Teorema della convergenza dominata: siano 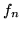 misurabili e
misurabili e
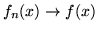 per ogni
per ogni 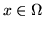 . Supponiamo che esista
. Supponiamo che esista
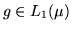 tale che per ogni
tale che per ogni  ed
ed 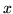 si abbia
si abbia
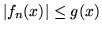 ; allora
; allora
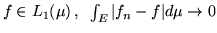 e inoltre
e inoltre
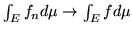 .
.
12. Sia P una proprietà che un punto 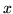 può avere o non avere. Si dice
che P vale quasi ovunque (q.o.) in un insieme
può avere o non avere. Si dice
che P vale quasi ovunque (q.o.) in un insieme 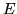 se il sottoinsieme di
se il sottoinsieme di 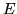 in cui
P non vale ha misura nulla. Gli insiemi di misura nulla sono trascurabili per
l'integrazione nel senso che se
in cui
P non vale ha misura nulla. Gli insiemi di misura nulla sono trascurabili per
l'integrazione nel senso che se 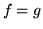 q.o. in
q.o. in 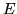 allora
allora
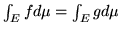 . Pertanto in questa teoria si parla spesso di funzioni definite q.o.
. Pertanto in questa teoria si parla spesso di funzioni definite q.o.
13. Una misura 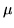 su una
su una 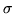 -algebra si dice completa se i sottoinsiemi
degli insiemi (misurabili) di misura nulla sono misurabili (e di misura nulla).
E' sempre possibile completare una misura ampliando in modo naturale la sua
-algebra si dice completa se i sottoinsiemi
degli insiemi (misurabili) di misura nulla sono misurabili (e di misura nulla).
E' sempre possibile completare una misura ampliando in modo naturale la sua
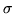 -algebra.
-algebra.
14. Sia 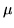 una misura di Borel. Un boreliano
una misura di Borel. Un boreliano 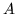 si dice
regolare se
si dice
regolare se
e se, nel caso che
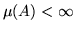 ,
,
Se ogni boreliano è regolare, 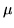 si dice regolare.
si dice regolare.
15. Ogni misura di Borel in 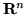 è regolare.
è regolare.



Next: Misura di Lebesgue
Up: Appendice
Previous: Appendice
Stefani Gianna
2000-11-06