Approssimazione normale

Spesso la tesi del Teorema Limite Centrale viene usata come una formula di approssimazione: si dice allora che si fa uso dell'approssimazione normale.
Il Teorema Limite Centrale afferma che

$$\lim_n \,p\,\{ \frac{X_1+..+X_n -\, n\mu}{\sigma \sqrt{n}} \l... ...{1}{\sqrt{2\pi}} \int_{-\infty}^t {\rm e}^{-\frac{y^2}{2}} dy .$$

Facendo uso dell'approssimazione normale porremo

$$p\,\{ \frac{X_1+..+X_n -\, n\mu}{\sigma \sqrt{n}} \leq t \} ... ...\pi}} \int_{-\infty}^t {\rm e}^{-\frac{y^2}{2}} dy = \Phi (t).$$

Pertanto se per un numero reale 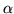$\alpha$ si deve stimare

$$A = p\,\{ X_1+..+X_n \leq \alpha \,\} \,,$$

tenuto conto che

$$\{ X_1+..+X_n \leq \alpha \,\} = \{ \frac{X_1+..+X_n -\, n\m... ...ma \sqrt{n}} \leq \frac{\alpha -\, n\mu}{\sigma \sqrt{n}} \}\,,$$

avremo

$$A \simeq \Phi (\frac{\alpha -\, n\mu}{\sigma \sqrt{n}}).$$

Se per esempio si vuole stimare una deviazione dalla media

$$D = p\{ \vert \frac{X_1+..+X_n }{n} - \mu\vert > c \,\}$$

come compare nella diseguaglianza di Chebyshev; si opera come segue:

$$D = 1 - p\{ X_1+..+X_n \leq n\mu +nc\,\} + p\{ X_1+..+X_n < n\mu - nc\,\} \simeq$$

$$\simeq 1 - \Phi (\frac{c \sqrt{n}}{\sigma}) + \Phi (-\frac{c \sqrt{n}}{\sigma}) = 2 \Phi (-\frac{c \sqrt{n}}{\sigma})\,.$$

Questa stima è in generale molto migliore di quella fornita dalla diseguaglianza di Chebyshev.
Tradizionalmente l'approssimazione normale si considera buona per gli 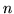$n$ maggiori di 50.