ACCELERAZIONE DEL PIEDE DI BIELLA

 

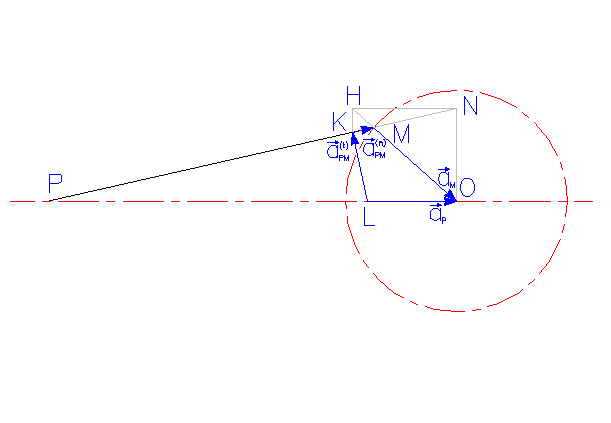
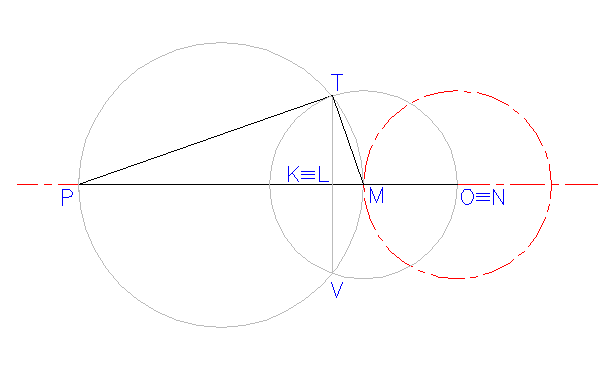
Cerchiamo ora una costruzione grafica per aP:

dove anPM ed atPM sono rispettivamente le accelerazioni normale e tangenziale di P relative ad M. Con la convenzione che le accelerazioni verranno riportate secondo la loro reale direzione e con la scala w2 = 1

aP = aM + anPM + atPM

 adesso sappiamo:

·     aM = OM   

·     i triangoli KMH ed MNO sono simili perché hanno i lati rispettivamente paralleli, per cui:  KM / MN = MH / MO

·     analogamente per i triangoli HNM e PMO : MH / MO = MN / MP

 Perciò:  KM = MN2 / MP = v2PM / PM = anPM
Sappiamo inoltre che atPM è diretta lungo KL ed aP lungo PO, quindi affinché sia verificata la relazione di partenza:

aP = LO

ed

atPM = LK
Questa costruzione cade però in difetto nei punti morti, dove il punto H è indeterminato. In tali posizioni vP = 0 , atPM = 0 , pertanto:

aP = aM + anPM      

con       

aM = MO
Il triangolo PTM ( vedere Fig ) è rettangolo perché inserito in una semicirconferenza, per il primo teorema di Euclide si ha: TM2 = KM * PM    

Þ     KM = TM2 / PM = vPM / PM = anPM   

Infatti:

vP = vPM + vM         

ma: vP = 0 , quindi:

vPM = vM = MO = TM    

Troviamo così:

  aP(q) = dvP(q) / dt = dvP(q) * w / dt = w2 r [ cos q + ( r cos (2q) ) / l ]
è da notare che questa costruzione detta di Klein, vale anche per altre configurazioni della biella.

 

Nelle pagine seguenti riportiamo la costruzione grafica per la determinazione dell’accelerazione del piede di biella