MOTI RIGIDI

1) Si definisce corpo rigido un qualsiasi corpo tale che, dati due punti P_i e P_j, ad esso appartenenti, sia

Analogamente è definito, moto di un corpo rigido L, lo studio del moto di un sistema solidale S, ad esso associato, rispetto ad un sistema fisso .
Per determinare il moto di un corpo rigido, costituito o meno da un numero finito di punti, è necessaria la conoscenza della configurazione e dell’ atto di moto iniziali di ogni punto del sistema.

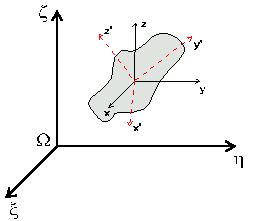
Sia L un corpo rigido, la velocità di un qualsiasi punto P del sistema solidale può essere espressa mediante la velocità del punto O di S rispetto a più un altro vettore dovuto alle variazioni dei versori solidali rispetto a .

Introduciamo a proposito il seguente Teorema (di Poisson):
In ogni moto rigido esiste uno ed un solo vettore  , dipendente dal tempo, tale che per ogni versore solidalesi ha

Dimostrazione
Poiché la derivata di un versore è sempre ortogonale al versore stesso, relativamente ad esisteranno opportuni vettori tali per cui

tenendo conto delle relazioni di ortogonalità fra i versori di una terna ortonormale

e derivando rispetto al tempo, si ha

Prendendo la prima relazione e lavorando su di essa, le altre seguiranno per analogia, si ottiene:

., ma   e , da cui

.

definendo le componenti di  e sostituendole nella relazione trovata:

., da cui, svolgendo i prodotti vettoriali,

., ed, infine, i prodotti scalari,

. ovvero .

Lavorando analogamente per le altre due relazioni si perviene al seguente risultato:

.;  ;  

ricapitolando i risultati ottenuti i tre vettori  si presentano nella forma

rimarrebbero da definire , ma la componente i-esima è sempre nulla ( infatti  )e quindi i vettori  possono essere definiti a meno di quella componente (che, quindi, sceglieremo uguale a quelle trovate),

.

Così facendo si ottiene:

. con .

Per ogni versore solidale  si ha

da cui

che raccolto a fattore è ovvero proprio come volevamo dimostrare.

Provatane l’ esistenza rimane da stabilire l’ unicità del vettore  per far questo si procederà supponendo l’ esistenza di un vettore che soddisfi, contemporaneamente ad, la relazione di Poisson:

. e 

ovvero

. da cui  o, meglio 

dall’ ultima relazione, per l’ arbitrarietà del vettor , si evince .

2)  

Per individuare la posizione del corpo L, istante per istante, sono sufficienti 3 coordinate per il punto O del sistema solidale (che forniscono la distanza del corpo dal sistema fisso), più gli angoli di Eulero per individuare la giacitura dei piani xy ; yz ; xz (che forniscono l’ orientazione del corpo rispetto al sistema fisso).

In tutto si tratta di 6 coordinate, esattamente tante quanti sono i gradi di libertà del corpo rigido nello spazio.

Preso un punto P appartenente al corpo rigido: vogliamo vedere come si muove P.

  1) Anzitutto si associa al punto P un vettore solidale come, ad esempio, (P-O)

  2) Si deriva rispetto al tempo: , ma, per Poisson è .

Rispetto a la rappresenta la velocità del punto P meno la velocità del punto O, ovvero

  , esplicitando la velocità del punto P, si ha

  (2.1)

  che rappresenta la legge di variazione del moto ed è la formula fondamentale dei moti rigidi.

Mediante questa legge è possibile esprimere le velocità di un qualsiasi punto P del sistemanS mediante la velocità di un altro punto O di S e del vettore  =  (non si dimentichi che O è un punto qualsiasi del sistema solidale e non necessariamente l’ origine) .

Per verificare la validità della formula dimostriamo che:

i) Se il moto è rigido, vale la (2.1).

i) Se vale la (2.1), allora il moto è rigido.

i) Supponendo il corpo rigido per ipotesi, è , derivando rispetto al tempo ed applicando Poisson si evince immediatamente la tesi.

ii) Posta valida per ipotesi la legge (2.1) mostriamo che il corpo altro non può essere che rigido.

., moltiplico scalarmente per (P-O)

.;

poiché , per cui rimane , ovvero:

 , Questa quantità è uguale a 0 e lo rimarrà anche moltiplicandola per,

  ., utilizzando una notazione un po' piratesca indichiamo questo termine come

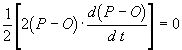  , che derivato da  , ovvero 

poiché la derivata è nulla, (P-O) deve rimanere costante nel tempo e, quindi, (il corpo è rigido).

I vettori ed che compaiono nella legge (2.1)(e dipendono generalmente dal tempo) caratterizzano completamente il moto rigido , e sono detti:

.Velocità di traslazione.

.Velocità di rotazione.

Assegnare la velocità di un qualsiasi punto O, e la velocità angolare , significa caratterizzare completamente uno degli moti possibili del sistema rigido.

L’ espressione dell’ accelerazione del punto P, rispetto a ,si ottiene derivando la (2.1) rispetto al tempo:

  (2.2)

L’ accelerazione di P è espressa in funzione della accelerazione del punto O, della velocità di rotazione  e della sua derivata . Il termine  è detto termine centripeto ed è diretto da P verso l’ asse parallelo ad  per O.

Si ponga attenzione al risultato intermedio ottenuto durante la dimostrazione della validità della (2.1) per il moto rigido:

  (2.3)

questa relazione afferma che le proiezioni del vettore e del vettore lungo la retta (P-O) sono uguali ciò vale per tutti i punti che appartengono alla stessa retta.

Il significato dell’ espressione è intuitivo: se la proiezione della velocità lungo la congiungente fra due punti fosse diversa, il corpo si romperebbe ed addio rigidità (come possono due punti rigidamente collegati, avere, nella stessa direzione, velocità diverse?).

Moltiplicando scalarmente la (2.1) per  si ha

. (2.4)

Questa relazione assicura che la componente della velocità, lungo il vettore , è sempre uguale per qualsiasi punto del corpo rigido (all’ istante t); stando così le cose questa componente (scalare) risulta invariante rispetto ad O, ed è detta invariante scalare del sistema L, all’ istante t; definiamo la componente  della velocità secondo la direzione :

questa componente, parallela ad , è detta invariante vettoriale.

3)

E’ possibile scomporre la velocità nelle due componenti, una parallela e l’ altra normale alla direzione di : ; in un punto P ho

  ma l’ espressione è tutta perpendicolare ad , è lecito chiedersi se esisteranno dei punti del corpo rigido per i quali questa espressione risulti nulla e l’ intera velocità si riduca alla sola componente parallela (sarà così trovato il luogo dei punti con velocità minima).

  ovvero .

quest’ ultima equazione equivale ad una relazione del tipo che, per il teorema di Rouché-Capelli ha soluzioni, il problema si riduce alla ricerca dei punti A tali per cui ; moltiplicando vettorialmente per 

,

  sfruttando le proprietà del doppio prodotto vettoriale,

  ,

  ed  sono perpendicolari e, dunque, il loro prodotto scalare è nullo, rimane

da cui

e, quindi, per l’anticommutatività del prodotto vettoriale.

  Se alla si aggiunge la , quest’ ultima non viene ad influire sul prodotto vettoriale, essendo parallela ad ; consente, però, di scrivere la formula generale:

. (3.1)

Tutti i punti passanti per A e giacenti sulla retta parallela ad  hanno velocità minima, questa retta prende il nome di asse di moto, che, dipendendo dal tempo, potrà essere diverso da istante ad istante, per cui si chiamerà asse istantaneo di moto.

L’ equazione dell’ asse sarà  con punto generico della retta, ed  soluzione della (3.1); in termini di coordinate, assumendo O come origine, siano  le componenti di , supposte tutte diverse da zero, l’ equazione della retta cercata sarà:

(3.2)

  con  risultati del prodotto vettoriale:

  ;  ; 

dove

  ed .

  La retta individuata prende il nome di asse istantaneo di moto, essa rappresenta il luogo geometrico dei punti che hanno solo velocità  e, come tale, la minima possibile rispetto ad ogni altro punto esterno ad essa.

Se la , allora i punti che le appartengono sono istantaneamente fermi.

Si noti che l’ esistenza di tale asse è assicurata ogni qualvolta sia .  

4)

Il luogo delle successive posizioni dell’asse di istantanea rotazione è una superficie rigata (qualsiasi superficie che si ottiene dal moto continuo di una retta si definisce rigata [cilindro, cono, ..]), infatti l’ equazione (3.2) rappresenta l’ intersezione di due piani:

piano  con il piano ;

un osservatore posto in (fisso) vedrà una superficie rigata detta rigata fissa del moto, un altro osservatore posto in S (solidale) vedrà, in genere, una rigata diversa detta rigata mobile del moto.

Rigata fissa e mobile hanno, all’ istante t, la stessa generatrice lungo la quale sono in contatto l’ una con l’ altra, essa è l’ asse istantaneo di moto.

I punti che appartengono a tale asse possono avere:

i) Velocità nulla, quando ;

ii) Velocità sempre parallela ad .

Durante il moto la rigata mobile ruota di un angolo attorno all’asse istantaneo di moto sulla rigata fissa nel tempo infinitesimo ; in questa rotazione vengono a contatto due nuove generatrici infinitamente vicine.

5)

Traslazioni

Il moto rigido conserva le direzioni ed in ogni istante si ha , chiaramente l’ asse istantaneo di moto rimane indeterminato.

Precessioni

Si chiama moto di precessione un qualunque moto rigido con un punto fisso.

Se O è il punto fisso ed , la formula fondamentale del corpo rigido diviene e l’ asse di istantanea rotazione passa per O. In questo caso le superfici rigate sono dei coni detti coni di Poinsot.

Rotazioni

La rotazione è un caso particolare di precessione con il vettore  che mantiene una direzione fissa.

Un qualsiasi punto P, esterno ad , descrive una circonferenza attorno ad esso, e per questo motivo  prende il nome di velocità di rotazione.

La matrice di rotazione propria (vedi angoli di Eulero) è una rotazione in z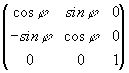 

Moti elicoidali

Il moto elicoidale è un moto rigido che mantiene fisso l’ asse di istantanea rotazione, ma ha invariante scalare  diverso da zero. Un esempio di moto elicoidale è il moto della vite.

E’ possibile richiamare il programma "MOVEAXIS"; dello studente Marco Martiri per la visione di solidi in moto di rotazione, precessione, per la visualizzazione delle due rigate, nonché delle intersezioni di queste con un piano perpendicolare all’ asse di rotazione.

Il programma è di utilizzo semplice ed intuitivo; utilizzare il cursore per muoversi all’ interno delle varie voci, ENTER come accettazione, ed il tasto ESC per cambiare vista prospettica durante l’ esecuzione del moto.