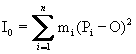
GEOMETRIA DELLE MASSE
Introduzione
Lo studio della distribuzione delle masse nei sistemi meccanici è di fondamentale importanza poiché da esso dipendono le proprietà geometriche e cinematiche dei sistemi stessi. Una volta note tali proprietà , non è difficile avere una visione completa della dinamica del sistema.
Dato un sistema di punti materiali, per avere informazioni sulla distribuzione di massa, definiamo i momenti di inerzia.
Momento polare
Dato un insieme di punti materiali Pi,mI, ed un punto fisso O, il momento polare rispetto ad O risulta essere:
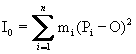
Momento assiale
Il momento assiale di un sistema di masse rispetto alla retta r è definito come
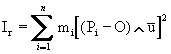
Momento planare
Il momento planare rispetto ad un piano p è definito come
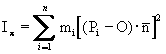
I momenti appena introdotti sono anche definiti come momenti del II ordine. Quelli del I ordine, detti statici, individuano il centro di massa P0:
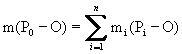
Ovviamente ogni momento di ordine superiore offre sempre più informazioni riguardo l’insieme delle distribuzioni possibili. Due sistemi con la stessa massa e stesso centro di massa, non necessariamente hanno identico momento del II ordine.
Struttura di inerzia
La struttura di inerzia è individuata dal momento del II ordine. Preso un corpo, sappiamo che per un punto passano ¥ 2 rette, poiché una volta fissato il punto ed individuati i coseni direttori a , b , g , la condizione a 2 +b 2 + g 2 =1 ci dice che la retta è individuata da due parametri. Se volessi conoscere I momenti rispetto alle rette per il punto O dovrei calcolare ¥ 2 momenti ?
Ciò rappresenta un processo infinito, dunque cerchiamo un modo più realistico per determinare la struttura di inerzia, intesa come momenti di inerzia rispetto a tutte le rette.
Fissata la terna di riferimento con centro in O ed assi (x, y, z), determiniamo i momenti di inerzia Ixx, Iyy, Izz, rispetto alle direzioni x, y, z. Tramite Pitagora otteniamo:
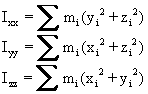
Il momento di inerzia rispetto ad una retta qualsiasi è
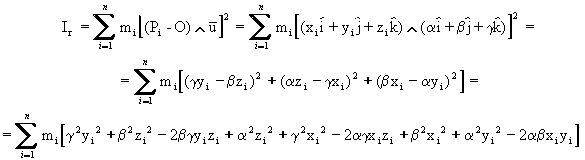
Poiché a , b , g , non dipendono dall’indice i, raccolgo i termini del secondo ordine ed ottengo
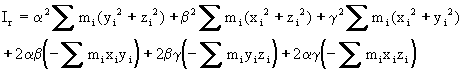
Il momento di inerzia rispetto alla retta r è una combinazione quadratica, definita positiva, in a , b , g , (si annulla solo in assenza di massa), abbiamo quindi:
![]()
dove Ixy , Iyz , Ixz , rappresentano il momento centrifugo, ovvero i momenti di inerzia rispetto alle coppie di piani di una terna ortogonale.
Più in generale definiamo il momento centrifugo rispetto al punto O, comune alla coppia di piani p e p‘ di un sistema di punti materiali
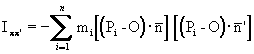
Da notare che il momento centrifugo è l’unico dei momenti del II ordine che può essere negativo.
Quindi noti Ixx, Iyy, Izz (momenti assiali) e Ixy , Iyz , Ixz (momenti centrifughi), posso conoscere il momento di inerzia rispetto a qualsiasi retta di cui sono noti i coseni direttori.
In conclusione la struttura di inerzia di un corpo è una grandezza nota se si conoscono i sei numeri che individuano i momenti assiali e centrifughi. Per definirla non è sufficiente né uno scalare, né un vettore poiché lavoriamo in R3, ma dobbiamo ricorrere all’utilizzo di una matrice che prende il nome di matrice d’inerzia. Poiché Iml = Iml , scriviamo:
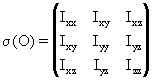
Tale matrice è un tensore del II ordine.
Metaforicamente possiamo vedere la matrice di inerzia come la carta di identità di una distribuzione di punti rispetto ad O.