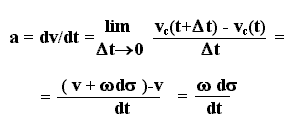Teorema di Eulero - Savary
|
Si
considerino le polari di un generico moto rigido piano e, in riferimento
alla Fig, assumiamo la curva l
come Base e l’
come Rulletta del moto considerato.
Sia
C il punto di contatto del rotolamento
puro delle due rigate, centro di istantanea
rotazione del moto.
In
corrispondenza di una rotazione infinitesima da
del piano mobile, C descriverà
un arco ds
sulla rulletta , in un tempo dt infinitesimo. |
|

|
| L’accelerazione
di C è nota in
direzione essendo normale alle due polari e in
modulo in quanto ottenuto nel seguente modo |
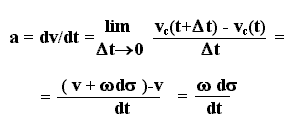
da = de - de’ = ds/r - ds/r’ = ds/D
con: 1/D = ( 1/r -
1/r’ )
|
| è
da notare che nella quantità D
il segno tra 1/r e 1/r’ è una differenza o un somma a seconda che le due polari
abbiano o non abbiano la stessa concavità. In definitiva risulta: |
aC = w r da/dt = w2
D |
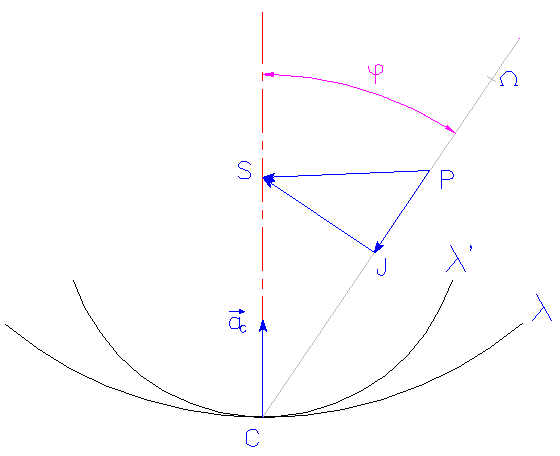
| Consideriamo adesso un generico punto P
appartenente al sistema rigido e calcoliamone l’accelerazione. |
aP
= aC + w Ù (P-C) + w Ù [ w Ù (P-C) ] |
|
|
| ma
prendendo un punto S tale che ôS-Cô = D si ha: |
aC
+ w Ù [ w Ù (P-C) ] = w2 (S-C) - w2 (P-C) = w2 (S-P) = w2 (S-J) + w2 (J-P)
|
| l’altro
termine è w
Ù (P-C)
ed è diretto ortogonale a (P-C)
e rappresenta una componente che chiamiamo tangenziale, si ottiene
quindi la seguente scomposizione dell’accelerazione del punto P: |
aP = aP(n)
+ aP(t) = w2 (J-P) + w2 (S-J) + w Ù (P-C) |
.
Se
P coincide con J
l’accelerazione normale di P è
nulla: il luogo dei punti sul piano che godono di questa proprietà è detto Circonferenza
dei flessi essendo infatti una circonferenza di diametro
D = SC
.
Tutti
i punti di questa circonferenza hanno esclusivamente accelerazione tangenziale e
quest’ultima passa costantemente per il punto S
( Polo dei flessi ).
Consideriamo
ora il centro di curvatura W
della traiettoria del punto P
all’istante considerato; esso dovrà appartenere alla retta CP
e la sua posizione può essere determinata considerando che:
aP(n) = vP2/r per cui
vP2/r = w2 CP2/ WP = w2 JP da cui
JP = CP2/ WP .
Adesso
si può dare anche una forma diversa scrivendo
infatti:
JP = JC + CP = Dcosj + CP
,
per
cui:
Dcosj = ( CP2/WP ) - CP ,
da
cui si ottiene una nuova formulazione del teorema
di Eulero - Savary:

1/D = [ ( 1/ CW ) - ( 1/ CP ) ]
.