Teoria geometrica del controllo - Controllo ottimo Programma del corso di dottorato - A.A. 2001/2002

Gianna Stefani

stefani@dma.unifi.it

Esempi introduttivi
Dal calcolo delle variazioni classico: problema di Didone, la brachistocrona, la catenaria.
Dalla geometria: le geodetiche riemanniane, le geodetiche subriemanniane.
Dalla meccanica: atterraggio morbido con vari criteri di ottimizzazione, barca che vuol raggiungere un approdo in tempo minimo, macchina di Dubins.
Dall'economia: modello di Ramsay di crescita economica.
Posizione del problema
Equazione di controllo, vincoli, costo sui punti estremi, costo integrale (running coast). Problemi in un intervallo di tempo variabile e in un intervallo di tempo fissato. Relazioni fra i vari tipi di problemi. Riduzione allo studio degli insiemi raggiungibili. Teoremi di esistenza.
Insiemi raggiungibili
Teorema delle orbite e sua relazione col teorema di Frobenious. Dimensione degli insiemi raggiungibili.
Il principio di massimo di Pontryagin
Hamiltoniane e sistemi Hamiltoniani. Il principio di massimo per problemi con intervallo di tempo fissato e variabile. Confronto con l'equazione di Eulero-Lagrange e con la funzione di eccesso di Weierstrass. Il problema degli estremali singolari nel caso del controllo.
Condizioni sufficienti
Principio di programmazione dinamica. Equazione di Hamilton-Jacobi-Bellmann. Metodi Hamiltoniani e loro relazione col metodo delle caratteristiche per la soluzione dell'equazione di Hamilton-Jacobi-Bellmann.
Eventuali ulteriori argomenti
Controllo ottimo in dimensione infinita e suo legame con il controllo delle equazioni alle derivate parziali
Soluzioni di viscosità dell'equazione di Hamilton-Jacobi-Bellmann e funzione obbiettivo.
Principi di massimo di ordine superiore.
Variazione seconda e punti coniugati.
 
Bibliografia molto parziale
L.S. Pontryagin, V. Boltyanskii, R.V. Gamkrelidze and E.F. Mishenko - "The Mathematical Theory of Optimal Processes, Wiley, 1962
E.B. Lee and L.Markus - "Foundations of Optimal Control Theory", Wiley, 1967
R.Conti - "Processi di Controllo Lineari in 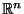$\R^n$, Quaderno UMI 30/1974
L. Cesari, "Optimization - Theory and Application", Spriger, 1983
V. Jurdjevich - "Geometric Control Theory", Cambridge University Press, 1997
 
Materiale di supporto da scaricare dalla rete
A.A. Agrachev and Yu.L. Sachov - "Lectures on Geometric Control Theory", Lectures Notes SISSA 38/2001/M
A. Bressan - "Viscosity solutionsof Hamilton Jacobi equations and optimal control", Lectures Notes SISSA 38/2001/M
H.J. Sussmann - "Corso all'istituto Weizmann", manoscritto.