Analisi II - Esercizi - 20-10-00 e 23-10-00
Serie numeriche
Serie telescopiche. Criterio del confronto asintotico.
Studio di convergenza di alcune serie numeriche.
Calcolo della somma quando possibile.
Successioni di funzioni
Riepilogo sulle definizioni dei vari tipi di convergenza: convergenza
puntuale, uniforme. Differenza tra convergenza uniforme su tutto 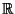 e convergenza uniforme sui compatti.
e convergenza uniforme sui compatti.
Serie di funzioni
Serie di potenze
- Calcolare il raggio di convergenza della serie
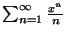
- Calcolare il raggio di convergenza della serie
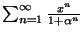 al variare di
al variare di
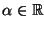 .
.
- Calcolare il raggio di convergenza della serie
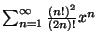
- Calcolare il raggio di convergenza della serie
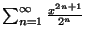
Somma di serie numeriche
Domini di funzioni da
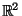 in
in 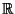 e
disequazioni in due variabili
e
disequazioni in due variabili
- Determinare il dominio di
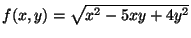
- Determinare il dominio di
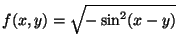
- Determinare il dominio di
![$f(x,y)=\log[\cos(x^2+y^2)]$](img45.gif)
- Determinare il dominio di
![$f(x,y)=\sqrt[3]{\log\left(\dfrac{x-y}{xy}\right)}$](img46.gif) .
.
- Determinare il dominio di
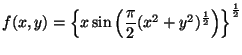
- Risolvere la disequazione
Limiti in
 e continuità
e continuità
- Studiare il comportamento in prossimità dell'origine della funzione
Suggerimento: provare prima avvicinandosi all'origine orizzontalmente,
verticalmente, lungo rette del tipo y=kx, quindi lungo la parabola
di equazione y=x2. Trarne le conclusioni.
Provare infine a fare i conti in coordinate polari e verificare che il
limite è zero per ogni 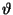 ma che non è uniforme.
ma che non è uniforme.
- Sia P=(x,y). Calcolare
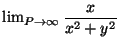 e
e
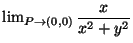 .
.
- Sia P=(x,y). Calcolare, se esiste
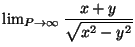
- Calcolare
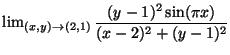 utilizzando le coordinate
polari.
utilizzando le coordinate
polari.
- Calcolare
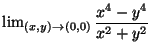 .
.
- Verificare che la funzione
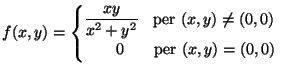 è continua separatamente nelle variabili x e y ma non è continua
come funzione di
è continua separatamente nelle variabili x e y ma non è continua
come funzione di
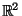 .
.
Francesco Mugelli
2000-10-25
![]() è crescente ed ha come limite il numero e.
è crescente ed ha come limite il numero e.
![]() è crescente ed ha come limite il numero e.
è crescente ed ha come limite il numero e.
![]() e convergenza uniforme sui compatti.
e convergenza uniforme sui compatti.
![$f(x,y)=\sqrt[3]{\log\left(\dfrac{x-y}{xy}\right)}$](img46.gif) .
.
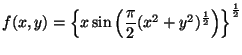
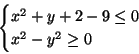
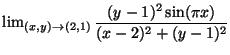 utilizzando le coordinate
polari.
utilizzando le coordinate
polari.
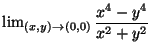 .
.
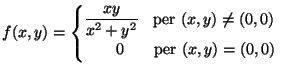 è continua separatamente nelle variabili x e y ma non è continua
come funzione di
è continua separatamente nelle variabili x e y ma non è continua
come funzione di