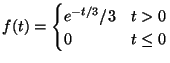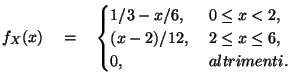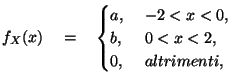

Next: About this document ...
Corsi di Laurea in Ingegneria Civile e Edile
Secondo
facsimile della prova intercorso sul Calcolo delle probabilita'
NOTA Le seguenti sono solo possibili tipologie di domande
1. Si intervista un campione di persone che escono da un certo negozio.
Di queste il  ha visto la pubblicità del negozio. Inoltre
il
ha visto la pubblicità del negozio. Inoltre
il 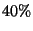 di tutto il campione ha fatto acquisti nel negozio.
I tre quarti di
quest'ultimi hanno visto la pubblicità del negozio.
Sulla base di questo campione, calcolare le probabilità:
di tutto il campione ha fatto acquisti nel negozio.
I tre quarti di
quest'ultimi hanno visto la pubblicità del negozio.
Sulla base di questo campione, calcolare le probabilità:
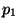 che una persona che ha visto la pubblicità faccia acquisti
nel negozio;
che una persona che ha visto la pubblicità faccia acquisti
nel negozio;
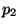 che una persona che non ha visto la pubblicità faccia acquisti.
che una persona che non ha visto la pubblicità faccia acquisti.
R1
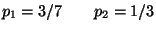
R2
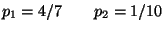
R3
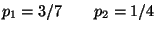
R4
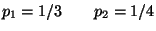
2. Un uomo va a pescare per la prima volta. Ha tre tipi di esche di cui
una sola è buona per pescare la trota. Sceglie l'esca a caso.
La probabilità di pescare una trota se usa l'esca corretta è di 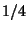 mentre se usa quella sbagliata è di
mentre se usa quella sbagliata è di 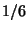 .
Qual è la probabilità,
.
Qual è la probabilità, 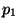 , di pescare una trota?
Supposto che la peschi, qual è la probabilità,
, di pescare una trota?
Supposto che la peschi, qual è la probabilità, 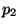 , che abbia usato
l'esca giusta?
, che abbia usato
l'esca giusta?
R1
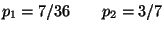
R2
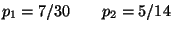
R3
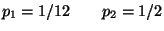
R4
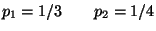
3. Siano 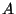 e
e 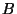 due eventi, e sia
due eventi, e sia 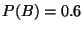 e
e
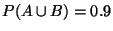 .
Quanto deve valere la probabilità
.
Quanto deve valere la probabilità 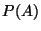 affinché
affinché 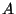 e
e 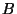 siano eventi statisticamente indipendenti?
siano eventi statisticamente indipendenti?
R1
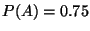
R2 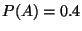
R3
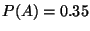
R4 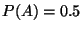
4. Sia 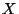 una variabile aleatoria discreta che assume i valori
una variabile aleatoria discreta che assume i valori
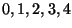 e per cui
dove
e per cui
dove 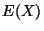 indica il valore atteso o media di
indica il valore atteso o media di 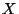 .
Trovare
.
Trovare
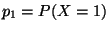 ,
,
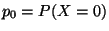 e
e
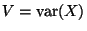 .
.
R1
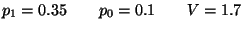
R2
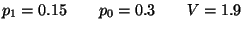
R3
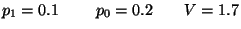
R4
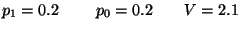
5. La variabile aleatoria 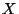 è distribuita secondo la distribuzione
normale con media 2 e deviazione standard 3. Quale delle seguenti affermazioni é corretta?
è distribuita secondo la distribuzione
normale con media 2 e deviazione standard 3. Quale delle seguenti affermazioni é corretta?
R1
![$ p(X\in [1,4])=p(N(0,1)\in [-1/3,2/3]) $](img35.gif)
R2
![$ p(X\in [1,4])=p(N(0,1)\in [1,4]) $](img36.gif)
R3
![$ p(X\in [1,4])=p(3N(0,1)\in [1,4]) $](img37.gif)
R4
![$ p(X\in [1,4])=p(N(0,9)\in [-1,2]) $](img38.gif)
6. Viene sviluppato un test che dovrebbe determinare la probabilità che un
topo sia fertile (risultato positivo). È stato stabilito che il
test risulta
negativo con probabilità 0.07 quando un topo fertile viene sottoposto
al test e risulta positivo con probabilità 0.04 quando un topo sterile
viene sottoposto al test. Determinare la probabilità 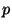 che un topo sia
fertile se il test risulta positivo dato che l'80% dei topi sono fertili.
che un topo sia
fertile se il test risulta positivo dato che l'80% dei topi sono fertili.
R1 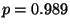
R2 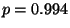
R3 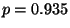
R4 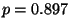
7. Il numero di macchine che passano per un certo punto di una strada della
città segue una distribuzione di Poisson di media 60 per ora. Determinare
la probabilità 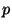 che esattamente una macchina passi per questo punto durante
un periodo di 10 minuti.
che esattamente una macchina passi per questo punto durante
un periodo di 10 minuti.
R1
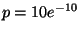
R2
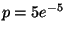
R3
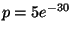
R4
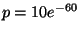
8. Nel corso di laurea il 60% degli studenti ha
fatto il liceo e l' 90% o ha fatto il liceo o è di sesso maschile
(``o'' non esclusivo).
Quale dovrebbe essere la percentuale dei maschi nel corso di laurea
affinché essere maschio e aver fatto il liceo siano due
eventi statisticamente indipendenti? (i dati sono fittizi)
R1 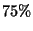
R2 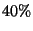
R3 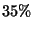
R4 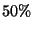
9. Una coppia decide di avere due figli e un'altra coppia di averne quattro.
La probabilità che nasca un maschio o una femmina è sempre del 50%.
Determinare la probabilità 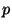 che ci siano meno di 3 figli maschi tra
le due famiglie.
che ci siano meno di 3 figli maschi tra
le due famiglie.
R1 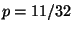
R2 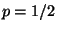
R3 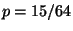
R4 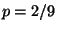
10. La durata 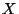 di un componente di un computer è una variabile aleatoria
con funzione di densità
dove il tempo
di un componente di un computer è una variabile aleatoria
con funzione di densità
dove il tempo 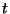 è misurato in anni. Determinare la durata media
è misurato in anni. Determinare la durata media 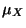 di un componente. Determinare la probabilità
di un componente. Determinare la probabilità 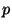 che un componente duri
più di 6 anni.
che un componente duri
più di 6 anni.
R1
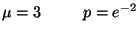
R2
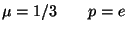
R3
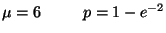
R4
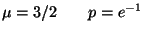
11. Sia 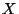 una variabile aleatoria continua con funzione di densità
Determinare la probabilità
una variabile aleatoria continua con funzione di densità
Determinare la probabilità 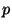 che
che 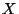 assuma valori tra 1 e 4.
assuma valori tra 1 e 4.
R1 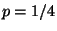
R2 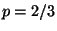
R3 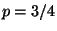
R4 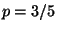
12. Luca lancia in aria una moneta non truccata quattro volte, senza mai
guardare il risultato. Il suo amico Giovanni gli dice che ha ottenuto
almeno due teste.
Determinare la probabilità 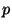 che Luca abbia ottenuto esattamente
tre teste.
che Luca abbia ottenuto esattamente
tre teste.
R1 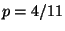
R2 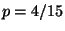
R3 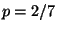
R4 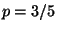
13. Sia 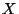 una variabile aleatoria con funzione di densità
con
una variabile aleatoria con funzione di densità
con 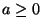 e
e 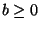 .
Determinare il valore atteso E
.
Determinare il valore atteso E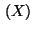 di
di 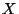 .
.
R1 E
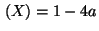
R2 E
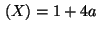
R3 E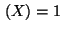
R4 E
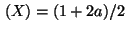
14.Un venditore ha deciso di accettare una consegna di 30 videoregistratori
solo se, scegliendo a caso un campione di 3 apparecchi, nessuno di questi
è difettoso.
Trovare la probabilità 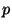 che il venditore accetti una consegna che
contiene 8 videoregistratori difettosi.
che il venditore accetti una consegna che
contiene 8 videoregistratori difettosi.
R1 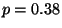
R2 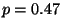
R3 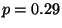
R4 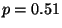
15.La durata di un dispositivo di allarme è una variabile aleatoria 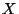 (
(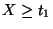 significa che il dispositivo si guasta per
significa che il dispositivo si guasta per 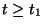 )
con densità
)
con densità
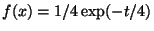 per
per 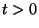 e
e 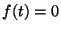 per
per 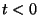 .
Calcolare
il tempo
.
Calcolare
il tempo 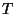 dopo il quale la probabilità che il dispositivo sia funzionante
diventa minore o uguale di
dopo il quale la probabilità che il dispositivo sia funzionante
diventa minore o uguale di 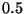
R1 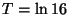
R2 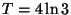
R3 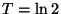
R4 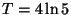


Next: About this document ...
Stefani Gianna
2001-01-24