
Next: About this document ...
Corsi di Laurea in Ingegneria Civile e Edile
Facsimile della prova intercorso sul Calcolo delle probabilita'
- Ogni inverno il 70% della popolazione prende un raffreddore, il 40%
prende un mal di gola e il 90% prende o l'uno o l'altro. Determinare la
probabilità
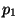 che una persona prenda tutti e due. Determinare la
probabilità
che una persona prenda tutti e due. Determinare la
probabilità 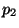 che una persona che prende un mal di gola prenda
anche un raffreddore.
che una persona che prende un mal di gola prenda
anche un raffreddore.
R1.

R2.

R3.
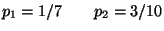
R4.
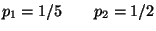
- Il 20% della popolazione di un'isola ha gli occhi blu.
Il Consiglio
Superiore dell'isola consiste di 10 membri. Determinare la probabilità
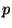 che almeno 2 fra di loro abbiano gli occhi blu. (Si può assumere
che il colore degli occhi non è un requisito per essere eletti nel
consiglio e che il consiglio sia composto solo da una piccola parte
della popolazione.)
che almeno 2 fra di loro abbiano gli occhi blu. (Si può assumere
che il colore degli occhi non è un requisito per essere eletti nel
consiglio e che il consiglio sia composto solo da una piccola parte
della popolazione.)
R1. 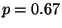
R2. 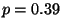
R3. 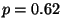
R4. 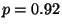
- In una scatola ci sono 300 semi di grano, di cui 120 sono stati trattati
con un antiparassitario. L'unico modo per determinare se un seme sia
stato trattato oppure no, è un test che rileva il trattamento con
probabilità del 95% nel caso di semi trattati, e che, nel caso
il seme non sia trattato, ha probabilità del 9% di dare una risposta
errata. Se un seme scelto a caso e sottoposto al test viene giudicato
"trattato", qual'è la probabilità che lo sia veramente?
R2. 92%
R1. 88%
R3. 95%
R4. Nessuna delle altre risposte
- Vengono condotte 6500 prove (indipendenti) di un esperimento con
probabilità di successo
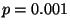 . Detto
. Detto 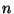 il numero dei successi
ottenuti, quale tra i seguenti è il valore di
il numero dei successi
ottenuti, quale tra i seguenti è il valore di 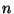 più probabile?
più probabile?
R1. 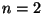
R2. 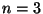
R3. 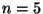
R4. 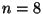
- Una lampadina ha una durata
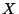 che è una variabile
aleatoria con funzione di densità
che è una variabile
aleatoria con funzione di densità
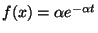 per
per 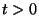 , con
, con 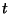 espesso in mesi. Quale deve essere il valore di
espesso in mesi. Quale deve essere il valore di
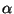 affinché la probabilità che la lampadina duri al più un
anno sia uguale al 60% ?
affinché la probabilità che la lampadina duri al più un
anno sia uguale al 60% ?
R1.
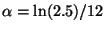
R2.
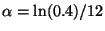
R3.
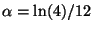
R4. Nessuna delle altre risposte
- In un'urna ci sono 7 palline bianche e 11 nere. Vengono estratte senza reimbussolamento
14 palline e si indica con
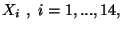 la variabile aleatoria che assegna
il valore 1 se la i-esima pallina estratta e' nera e 0 altrimenti. Calcolare il coefficiente
di correlazione di
la variabile aleatoria che assegna
il valore 1 se la i-esima pallina estratta e' nera e 0 altrimenti. Calcolare il coefficiente
di correlazione di 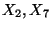
R1. 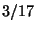
R2. 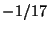
R3. 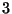
R4. 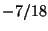
- La deviazione standard della densita' geometrica
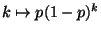 di parametro
di parametro 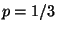 e':
e':
R1. 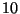
R2. 
R3. 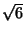
R4. Nessuna delle altre risposte
- Quattro persone giocano a poker con un mazzo di 52 carte a cui sono state tolte
le carte dal due al sei. Che probabilita' si ha che il maziere abbia
colore servito?
(a poker si danno 5 carte, il colore consiste nell'avere tutte e 5 le
carte dello
stesso seme)
R1. 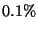
R2. 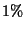
R3. 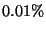
R4. Nessuna delle altre risposte
- Per una ricerca statistica si e' divisa una popolazione in tre fasce A, B, C contenenti
il 40%, 35% e il 25% della popolazione totale rispettivamente.
Nella fascia A sono state messi gli individui che fumano meno di 5 sigarette al
giorno, nella fascia B quelli che ne fumano da 5 a 20, nella fascia C quelli che ne
fumano piu' di 20. Si sono presi in considerazione gli individui ammalati di una malattia
polmonare cronica che sono il 30% della popolazione e si e'
calcolato che il 40% di questi appartiene alla fascia C,
il 35% alla fascia B e il 25% alla fascia A. Calcolare la probabilita'
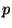 che
un individuo che non fuma si ammali e la probabilita'
che
un individuo che non fuma si ammali e la probabilita' 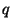 che un individuo
che fuma
30 sigarette al giorno si ammali.
che un individuo
che fuma
30 sigarette al giorno si ammali.
R1.
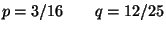
R2.

R3.
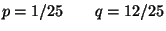
R4.

- La densita' congiunta di due v.a.
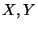 e' la densita' uniforme sull'ellisse
di equazione
e' la densita' uniforme sull'ellisse
di equazione
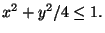 Calcolare
Calcolare
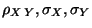
R1.
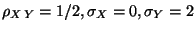
R2.
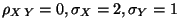
R3.
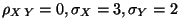
R4.
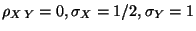
- Per quali valori del parametro
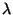 la funzione
rappresenta la densita' di una v.a. continua?
la funzione
rappresenta la densita' di una v.a. continua?
R1.
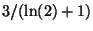
R2.
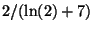
R3.
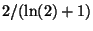
R4.
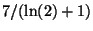


Next: About this document ...
Stefani Gianna
2001-01-18