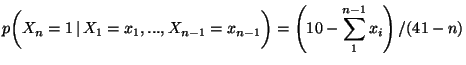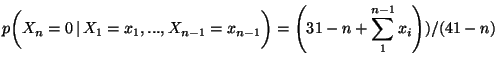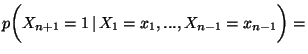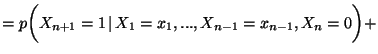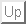

Next: About this document ...
Corsi di Laurea in Ingegneria Civile e Edile
Esercizi di Calcolo delle Probabilita' 3/1/01
- Calcolare media, varianza e deviazione standard della densita' geometrica
di parametro
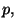 si ricorda che la densita' geometrica vale
si ricorda che la densita' geometrica vale
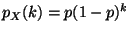 .
.
Suggerimento: Nel calcolo della somma delle serie si considerino le proprieta'
delle serie di Taylor e il fatto che
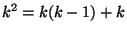
- Calcolare covarianza e coefficiente di correlazione delle seguenti
coppie di v.a. che si suppongono a media e varianza finita
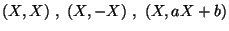 con
con
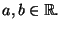
- Da un mazzo di
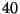 carte si pescano successivamente due carte, senza rimettere
nel mazzo la prima carta. Indichiamo con
carte si pescano successivamente due carte, senza rimettere
nel mazzo la prima carta. Indichiamo con
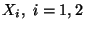 la v.a. che assume il
valore
la v.a. che assume il
valore 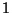 se si pesca cuori la
se si pesca cuori la 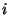 -esima volta.
-esima volta.
a) Calcolare la probabilita'
marginale, media, varianza e deviazione standard di ciascuna delle 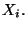
b) Calcolare la probabilita' congiunta, la covarianza e il coefficiente di correlazione
di
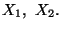 c) Calcolare la media e la varianza di
c) Calcolare la media e la varianza di 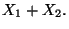
Suggerimento: a) Si verifichi che
- Ripetere il precedente esercizio con un mazzo di 52 carte.
- Si distribuisce un mazzo di
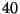 carte e si indica
con
carte e si indica
con
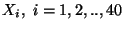 la v.a. che assume il
valore
la v.a. che assume il
valore 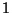 se si ha cuori nella
se si ha cuori nella 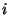 -esima carta (si tratta di
-esima carta (si tratta di 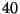 prove
dipendenti di un esperimento di Bernulli).
prove
dipendenti di un esperimento di Bernulli).
a)
Calcolare la probabilita'
marginale, media, varianza e deviazione standard di ciascuna
delle
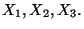
b) Verificare il fatto intuitivo
che la probabilita' marginale di ciascuna delle 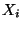 coincide con
quella di
coincide con
quella di 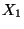 e che la probabilita' congiunta di
e che la probabilita' congiunta di
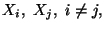 coincide con quella di
coincide con quella di
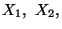 vedi anche es.3.
vedi anche es.3.
c) Calcolare la probabilita' congiunta, la covarianza e il coefficiente di correlazione
di
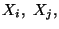
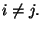 Calcolare la media e la varianza di
Calcolare la media e la varianza di 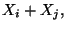
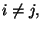 vedi anche es.3.
vedi anche es.3.
Suggerimento: b) Basta dimostrare che se 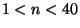 La probabilita' di
La probabilita' di 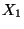 e'
e' 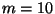 su
su 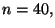 tutte le volte che si distribuisce una carta,
tutte le volte che si distribuisce una carta, 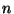 diminuisce di
diminuisce di 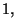 se la carta e' cuori, cioe' il valore della v.a. e'
se la carta e' cuori, cioe' il valore della v.a. e' 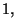 anche
anche 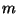 diminuisce di
diminuisce di 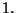 Quindi
Quindi
- Si distribuisce un mazzo di
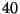 carte fra quattro persone e si indica
con
carte fra quattro persone e si indica
con
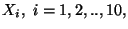 la v.a. che assume il
valore
la v.a. che assume il
valore 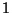 se si ha cuori nella
se si ha cuori nella 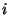 -esima carta del maziere (del primo, secondo
terzo giocatore).
-esima carta del maziere (del primo, secondo
terzo giocatore).
a) Calcolare la probabilita'
marginale, media, varianza e deviazione standard di ciascuna delle 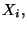 e la probabilita' congiunta di
e la probabilita' congiunta di
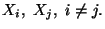
b) Calcolare la probabilita' che il maziere abbia 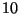 carte di cuori
(vedi anche es.4 del Dott. Mugelli)
carte di cuori
(vedi anche es.4 del Dott. Mugelli)
c) Calcolare la probabilita' che il maziere abbia 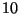 carte dello stesso seme
(vedi anche es.4 del Dott. Mugelli)
carte dello stesso seme
(vedi anche es.4 del Dott. Mugelli)
Suggerimento: a) Ricondursi all'esercizio precedente.
b) La v.a. che descrive il problema e'
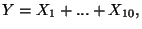 che e' una v.a. ipergeometrica
che e' una v.a. ipergeometrica
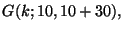 si tratta di calcolare
si tratta di calcolare
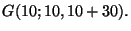
c) Poiche' avere 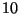 carte di cuori e' un evento disgiunto da avere
carte di cuori e' un evento disgiunto da avere 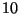 carte di
picche etc.., otterremo la probabilta' come
carte di
picche etc.., otterremo la probabilta' come
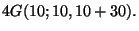
- Ripetere gli esercizi precedenti con un mazzo di
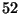 carte
carte
- Nel gioco del Bridge una linea di gioco,
diciamo giocatori A e B, ha due picche. Calcolare la probabilita' che A abbia
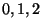 picche (vedi anche es.1 del Dott. Mugelli).
picche (vedi anche es.1 del Dott. Mugelli).
Suggerimento: Nella linea si hanno 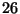 carte di cui
carte di cui 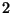 picche, si
tratta di vedere le possibilita' di avere le picche scegliendo a caso
picche, si
tratta di vedere le possibilita' di avere le picche scegliendo a caso 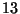 carte su
carte su 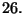 Si deve cioe' calcolare la densita' ipergeometrica
Si deve cioe' calcolare la densita' ipergeometrica
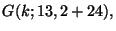 per
per 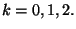
- Nel gioco del Bridge una linea di gioco,
diciamo giocatori A e B, ha sei fiori.
a) Calcolare la probabilita' che A abbia
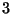 fiori (vedi anche es.2 del Dott. Mugelli).
fiori (vedi anche es.2 del Dott. Mugelli).
b) Sapendo che A ha la Donna, calcolare la probabilita' che sia seconda.
Suggerimento: a) Analogamente all'esercizio precedente si deve
calcolare la densita' ipergeometrica
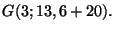
b) Si tratta di calcolare la probabilita' di avere una fiori su 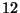 carte scelte tra
carte scelte tra 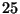 di cui
di cui 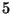 fiori.
fiori.
- Ripetere gli esercizi precedenti per il gioco del Tressette, cioe' con un mazzo
di
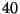 carte (vedi anche es.3 del Dott. Mugelli).
Vedere come variano le probabilita' in funzione del numero
carte (vedi anche es.3 del Dott. Mugelli).
Vedere come variano le probabilita' in funzione del numero 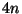 di carte.
di carte.
- Da un'urna contenente
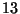 palline bianche,
palline bianche, 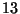 palline rosse,
palline rosse,
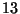 palline gialle e
palline gialle e 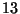 palline verdi, si estraggono
palline verdi, si estraggono 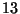 palline.
Calcolare la probabilita' di estrarre
palline.
Calcolare la probabilita' di estrarre 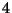 palline bianche,
palline bianche, 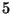 palline rosse,
palline rosse,
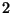 palline gialle e
palline gialle e 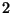 palline verdi (vedi anche es.5 del Dott. Mugelli).
palline verdi (vedi anche es.5 del Dott. Mugelli).
Suggerimento: Si tratta di calcolare come si possono estrarre
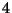 palline bianche su
palline bianche su 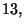
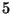 palline rosse su
palline rosse su 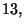
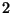 palline gialle su
palline gialle su 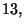
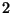 palline verdi su
palline verdi su 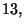 su le possibilita' totali
di estrazione di
su le possibilita' totali
di estrazione di 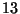 palline su
palline su 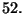
- In un'urna sono contenute
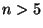 palline numerate da
palline numerate da  a
a
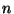 . Si estraggono tutte le palline e un giocatore punta alla pari
che le palline
. Si estraggono tutte le palline e un giocatore punta alla pari
che le palline 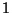 e
e 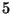 vengano estratte consecutivamente. Per quali valori
di
vengano estratte consecutivamente. Per quali valori
di 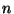 il gioco e' equo? (vedi anche es.6 del Dott. Mugelli).
il gioco e' equo? (vedi anche es.6 del Dott. Mugelli).
Suggerimento: Le possibili estrazioni sono 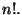 Fissata la posizione di
Fissata la posizione di 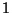 e
e 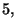 mediante la posizione di
mediante la posizione di 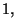 si tratta di calcolare
come si possono estrarre le
rimanenti
si tratta di calcolare
come si possono estrarre le
rimanenti 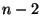 palline ( sono
palline ( sono 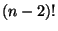 ) e poi di valutare le possibili
posizioni di
) e poi di valutare le possibili
posizioni di
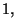 che sono
che sono 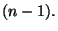
Si noti che nel caso del mazzo di carte se si punta sui valori,
il numero delle possibili posizioni va moltiplicato per 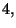 numero dei semi.
numero dei semi.
- Due urne contengono ciascuna
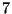 elementi denotati
elementi denotati
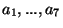 .
Da ogni urna si estraggono
.
Da ogni urna si estraggono 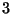 elementi, calcolare la probabilita' di non avere
elementi comuni fra le due estrazioni. Calcolare la probabilita' di avere elementi
elementi, calcolare la probabilita' di non avere
elementi comuni fra le due estrazioni. Calcolare la probabilita' di avere elementi
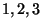 elementi comuni fra le due estrazioni.
elementi comuni fra le due estrazioni.
- Un mazzo di
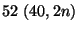 carte viene distribuito. Calcolare la probabilita' che
la prima e l'ultima carta abbiano lo stesso colore, siano rosse, siano di colori
diversi.
carte viene distribuito. Calcolare la probabilita' che
la prima e l'ultima carta abbiano lo stesso colore, siano rosse, siano di colori
diversi.
Suggerimento: Tenere conto dell'esercizio 5.
- Da un mazzo di
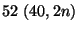 si toglie una carta rossa e si distribuisce.
Calcolare la probabilita' che
la prima e l'ultima carta siano rosse, siano nere, abbiano lo stesso colore, siano di colori
diversi.
si toglie una carta rossa e si distribuisce.
Calcolare la probabilita' che
la prima e l'ultima carta siano rosse, siano nere, abbiano lo stesso colore, siano di colori
diversi.
- Un'urna contiene
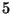 palline rosse e
palline rosse e 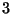 bianche.
bianche.
a) Si lancia una volta un dado
e si estrae un numero di palline pari al risultato. Calcolare la probabilita'
di estrarre solo 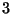 palline rosse, che fra le palline estratte ce ne siano esattamente
(almeno, al piu')
palline rosse, che fra le palline estratte ce ne siano esattamente
(almeno, al piu') 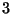 rosse.
rosse.
b) Si lancia due volta il dado
e si estrae ogni volta un numero di palline pari al risultato. Calcolare la probabilita'
di estrarre solo palline rosse, che fra le palline estratte ce ne siano esattamente
(almeno, al piu') 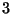 rosse.
rosse.
- Si fanno tre lanci successivi di un dado, calcolare la probabilita' che escano
tre risultati uguali.
- In una estrazione con reimbussolamento di
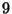 oggetti su
oggetti su 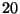 si punta sull'uscita di
si punta sull'uscita di 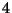 oggetti fissati. Quanto deve essere la quota concessa dal
"banco" perche' il gioco sia equo?
oggetti fissati. Quanto deve essere la quota concessa dal
"banco" perche' il gioco sia equo?
- In un negozio si vendono computer di tre marche diverse, chiamate A,B,C,
in percentuali del
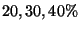 rispettivamente. Le percentuali di computer
non funzionati per le tre marche e' rispettivamente del
rispettivamente. Le percentuali di computer
non funzionati per le tre marche e' rispettivamente del 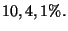 Calcolare la probabilita' che un computer (non) funzionante venduto nel
negozio sia stato prodotto dalla marca A (B,C,).
Calcolare la probabilita' che un computer (non) funzionante venduto nel
negozio sia stato prodotto dalla marca A (B,C,).


Next: About this document ...
Stefani Gianna
2001-01-15