

Next: About this document ...
truept
Corsi di Laurea in Ingegneria Civile e Edile
Analisi Matematica
II e Probabilita'
Prof. G. Stefani
Esercizi svolti o proposti a lezione dal 21 al 24/11/00
- Calcolare l'approssimazione di Taylor centrata in (0,0) di ordine 4
della funzione
- Data la funzione
e l'insieme
determinare gli estremi superiore e inferiore di 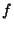 su
su 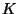 e gli eventuali massimi e
minimi globali (assoluti) su
e gli eventuali massimi e
minimi globali (assoluti) su 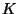 e su
e su 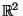 .
.
- Verificare che in
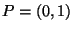 le ipotesi del teorema della funzione implicita (Dini)
per la funzione
le ipotesi del teorema della funzione implicita (Dini)
per la funzione
Disegnare il grafico della funzione implicita
definita da
vicino al punto 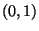 mettendo in evidenza crescenza, decrescenza, concavita',
convessita'.
mettendo in evidenza crescenza, decrescenza, concavita',
convessita'.
- Determinare gli eventuali massimi e minimi locali della funzione
vincolata a
- Determinare gli eventuali massimi e minimi globali (assoluti) della funzione
vincolata a
- Calcolare
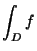 se
se
- Verificare che
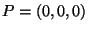 soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per l'equazione
soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per l'equazione
Calcolare il polinomio di taylor di ordine due centrato in 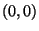 della funzione implicita
definita da
della funzione implicita
definita da
- Verificare che esiste un unico
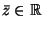 tale che
tale che
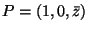 che soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per l'equazione
che soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per l'equazione
Calcolare il polinomio di taylor di ordine due centrato in 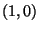 della funzione implicita
definita da
della funzione implicita
definita da
- Verificare che per ogni
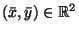 esiste un unico
esiste un unico 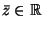 tale che
tale che
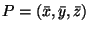 che soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per la funzione
che soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per la funzione
Calcolare il polinomio di taylor di ordine due centrato in
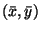 della funzione implicita
definita da
della funzione implicita
definita da
- Verificare che
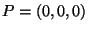 soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per la funzione
soddisfa
le ipotesi del teorema della funzione implicita (Dini)
per la funzione
Determinare i valori del parametro 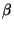 per cui la funzione implicita
definita da
per cui la funzione implicita
definita da
ha un minimo relativo in 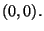
- Determinare il baricentro della regione limita di piano compresa fra le curve
- Considerare il problema di massimizzare la funzione
con il vincolo
Verificare che
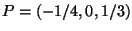 e' l'unico punto che verifica le condizioni
necessarie
del primo ordine del problema vincolato e non quelle del problema libero.
e' l'unico punto che verifica le condizioni
necessarie
del primo ordine del problema vincolato e non quelle del problema libero.
- Determinare il dominio di integrazione come integrale doppio dell'integrale
iterato
e cambiare ordine di integrazione.


Next: About this document ...
Stefani Gianna
2000-11-24