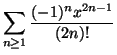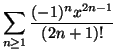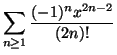

Next: About this document ...
Analisi Matematica II - C.d.L. Civile ed Edile
Prova A del 9/04/01. Durata: ore
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
ES.1 Sia
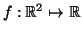 definita da
definita da
- a.
- Calcolare, se esiste,
- b.
- Determinare gli eventuali massimi e minimi locali.
- c.
- In quali punti di quali linee di livello di
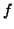 non si puo' applicare il
teorema della funzione implicita?
non si puo' applicare il
teorema della funzione implicita?
ES.2
Determinare il raggio di convergenza e la somma della serie
Analisi Matematica II - C.d.L. Civile ed Edile
Prova B del 9/04/01. Durata: ore
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
ES.1 Sia
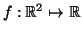 definita da
definita da
- a.
- Calcolare, se esiste,
- b.
- Determinare gli eventuali massimi e minimi locali.
- c.
- In quali punti di quali linee di livello di
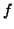 non si puo' applicare il
teorema della funzione implicita?
non si puo' applicare il
teorema della funzione implicita?
ES.2
Determinare il raggio di convergenza e la somma della serie
Analisi Matematica II - C.d.L. Civile ed Edile
Prova C del 9/04/01. Durata: ore
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
ES.1 Sia
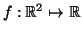 definita da
definita da
- a.
- Calcolare, se esiste,
- b.
- Determinare gli eventuali massimi e minimi locali.
- c.
- In quali punti di quali linee di livello di
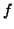 non si puo' applicare il
teorema della funzione implicita?
non si puo' applicare il
teorema della funzione implicita?
ES.2
Determinare il raggio di convergenza e la somma della serie
Calcolo delle probabilita' - C.d.L. Civile ed Edile
Prova orale A del 9/04/01. Durata: ore
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
Sia 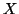 una variabile aleatoria di densita'
una variabile aleatoria di densita'
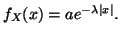
- a.
- Determinare
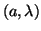 sapendo che
sapendo che
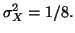
- b.
- Disegnare il grafico della funzione densita' e della funzione
di ripartizione di
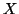 e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
- c.
- Calcolare
![$ p(X\in [-1,2]).$](img14.gif)
Calcolo delle probabilita' - C.d.L. Civile ed Edile
Prova orale B del 1/02/01. Durata: ore
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
ES.1
Sia 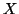 una variabile aleatoria normale di media
una variabile aleatoria normale di media  e varianza
e varianza 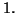
- a.
- Disegnare il grafico della funzione densita' e della funzione
di ripartizione di
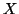 e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
- b.
- Sia
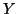 una variabile aleatoria normale di media 0 e varianza
una variabile aleatoria normale di media 0 e varianza 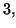 indipendente da
indipendente da 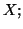 calcolare la
probabilita' che la coppia
calcolare la
probabilita' che la coppia 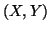 disti dal punto
disti dal punto 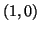 meno di
meno di 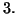
Calcolo delle probabilita' - C.d.L. Civile ed Edile
Prova orale C del 9/04/01. Durata: ore
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
ES.1
Sia 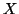 una variabile aleatoria esponenziale di parametro
una variabile aleatoria esponenziale di parametro
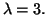
- a.
- Disegnare il grafico della funzione densita' e della funzione
di ripartizione di
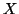 e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
- b.
- Sia
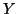 una variabile aleatoria esponenziale di media
una variabile aleatoria esponenziale di media 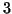 e indipendente
da
e indipendente
da 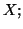 calcolare la
probabilita'
calcolare la
probabilita'
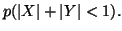


Next: About this document ...
Stefani Gianna
2001-04-18