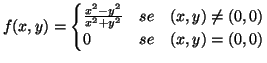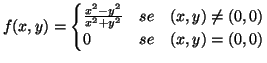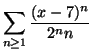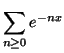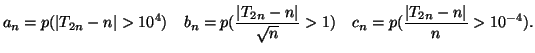

Next: About this document ...
Analisi Matematica II e Calcolo delle probabilita' - C.d.L. Civile ed Edile
Prova orale A del 1/02/01. Durata: ore 2
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
Per superare la prova orale e' necessario rispondere a qualche quesito
in ciascuno dei tre esercizi.
ES.1 (tempo consigliato : 45 minuti) Sia
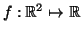 definita da
definita da
- a.
- Determinare l'insieme in cui
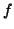 e' differenziabile.
e' differenziabile.
- b.
- Discutere la limitatezza e l'esistenza di massimo e minimo globali
(si consiglia di passare in coordinate polari).
- c.
- Calcolare la derivata di
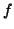 in direzione del vettore
in direzione del vettore
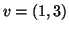 nel punto
nel punto 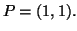
- d.
- Sia
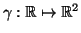 definita da
definita da
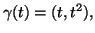 calcolare la derivata di
calcolare la derivata di
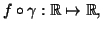 nel
punto
nel
punto 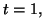 e la matrice Jacobiana di
e la matrice Jacobiana di
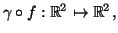 nel punto
nel punto 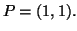
- e.
- Calcolare la retta tangente alla curva di livello
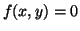 nel punto
nel punto 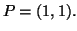
- f.
- Enunciare il teorema della funzione implicita per la curva di livello
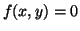 nel punto
nel punto 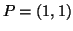 e dedurne il grafico vicino a
e dedurne il grafico vicino a 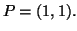
- g.
- Quali sono i punti di
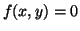 in cui non si puo' applicare il
teorema della funzione implicita?
in cui non si puo' applicare il
teorema della funzione implicita?
ES.2 (tempo consigliato : 30 minuti)
Considerare la serie di potenze
- a.
- Calcolare il raggio di convergenza
- b.
- Determinarne l'intervallo in cui la serie converge puntualmente.
- c.
- La serie converge uniformemente in
![$ [6,8]$](img14.gif) ?
?
- d.
- Determinare gli intervalli in cui la serie converge uniformemente.
- e.
- Definire il raggio di convergenza.
- f.
- Calcolare la somma della serie, specificando l'insieme su cui
l'uguaglianza e' verificata.
ES.3 (tempo consigliato : 45 minuti)
Sia 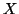 una variabile aleatoria normale di media
una variabile aleatoria normale di media 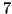 e varianza
e varianza 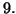
- a.
- Disegnare il grafico della funzione densita' e della funzione
di ripartizione di
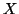 e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
- b.
- Detta
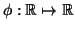 la funzione di ripartizione di
la funzione di ripartizione di 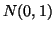 (normale standard), calcolare
(normale standard), calcolare
![$ p(X\in [-3,3])$](img20.gif) in termini di
in termini di 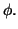
- c.
- Sia
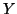 una variabile aleatoria con la stessa legge di
una variabile aleatoria con la stessa legge di 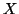 e da
questa indipendente, calcolare la
probabilita' che la coppia
e da
questa indipendente, calcolare la
probabilita' che la coppia 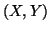 disti dal punto
disti dal punto 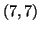 meno di
meno di 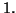
- d.
- Enunciare il teorema del limite centrale e, usando l'approssimazione
normale, calcolare la probabilita' che su
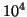 lanci di una moneta
equilibrata escano un numero di teste comprese fra
lanci di una moneta
equilibrata escano un numero di teste comprese fra 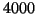 e
e 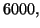 esprimendola
mediante
esprimendola
mediante 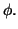
- e.
- Sapendo che
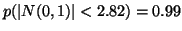 (praticamente uno) in quale
intervallo ci si deve aspettare il numero di teste del precedente esperimento?
(praticamente uno) in quale
intervallo ci si deve aspettare il numero di teste del precedente esperimento?
Analisi Matematica II e Calcolo delle probabilita' - C.d.L. Civile ed Edile
Prova orale A del 1/02/01. Durata: ore 2
Rispondere ai seguenti quesiti giustificando le risposte.
Risposte senza giustificazione non verranno ritenute valide.
Per superare la prova orale e' necessario rispondere a qualche quesito
in ciascuno dei tre esercizi.
ES.1 (tempo consigliato : 45 minuti) Sia
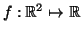 definita da
definita da
- a.
- Calcolare, se esiste,
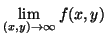 e dare la definizione di
e dare la definizione di
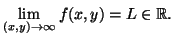
- b.
- Discutere l'esistenza di massimo e minimo della funzione nel cerchio chiuso
di centro l'origine e raggio 2 e nel cerchio aperto.
- c.
- Discutere la limitatezza di
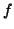 e l'esistenza di massimo e minimo globali
(si consiglia di passare in coordinate polari).
e l'esistenza di massimo e minimo globali
(si consiglia di passare in coordinate polari).
- d.
- Calcolare la derivata di
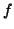 in direzione del vettore
in direzione del vettore
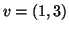 nel punto
nel punto 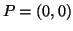 e il piano tangente al grafico della funzione
nel punto di coordinate
e il piano tangente al grafico della funzione
nel punto di coordinate 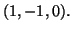
- e.
- Sia
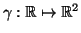 definita da
definita da
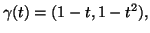 calcolare la derivata di
calcolare la derivata di
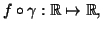 nel
punto
nel
punto 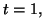 e la matrice Jacobiana di
e la matrice Jacobiana di
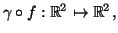 nel punto
nel punto 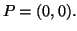
- f.
- Calcolare il polinomio di taylor del secondo ordine di
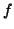 centrato
nell'origine.
centrato
nell'origine.
- g.
- Enunciare le condizioni necessarie e le condizioni sufficienti
affinche' un punto
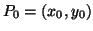 sia un massimo o un minimo locale
per
sia un massimo o un minimo locale
per 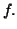 Determinare i punti stazionari della
Determinare i punti stazionari della 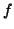 e studiarli.
e studiarli.
ES.2 (tempo consigliato : 30 minuti)
Considerare la serie di funzioni
- a.
- Calcolare l'insieme in cui la serie converge puntualmente.
- b.
- La serie converge uniformemente in
![$ [1,6]$](img40.gif) ?
?
- c.
- Determinare gli intervalli in cui la serie converge uniformemente.
- d.
- Definire il significato di
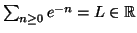
- e.
- Calcolare la somma della serie, specificando l'insieme su cui
l'uguaglianza e' verificata.
ES.3 (tempo consigliato : 45 minuti)
Sia 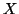 una variabile aleatoria esponenziale di parametro
una variabile aleatoria esponenziale di parametro
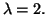
- a.
- Disegnare il grafico della funzione densita' e della funzione
di ripartizione di
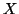 e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
e definire la funzione di ripartizione in termini di
probabilita' e di densita'.
- b.
- Sia
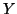 una variabile aleatoria con la stessa legge di
una variabile aleatoria con la stessa legge di 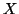 e da
questa indipendente, calcolare la
probabilita'
e da
questa indipendente, calcolare la
probabilita'
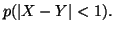
- c.
- Enunciare il teorema del limite centrale. Detto
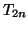 il numero
di teste ottenute su
il numero
di teste ottenute su 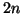 lanci di una moneta
equilibrata,
usando l'approssimazione
normale e la funzione di ripartizione
lanci di una moneta
equilibrata,
usando l'approssimazione
normale e la funzione di ripartizione 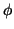 di
di 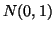 (normale standard),
calcolare le probabilita'
calcolare
(normale standard),
calcolare le probabilita'
calcolare
 e discutere il
risultato confrontandolo con la legge dei grandi numeri.
e discutere il
risultato confrontandolo con la legge dei grandi numeri.


Next: About this document ...
Stefani Gianna
2001-06-19