Francesco Ricci

Complex networks

The emerging properties on complex networks play a central role in several domains, such as neuroscience, technology, communication or physics. The majority of researchers have been focused on networks whose structure is static, but in nature the connectivity and coupling strengths of a networks cannot always be assumed constant in time. Typically, the network topology evolves in time to optimise certain network functions. Here we find two different competing dynamics: the dynamics on each node and the dynamic of the network structure. The main goal in my research is to study the emergence of collective properties in evolving complex networks of particular interest when the nodes and structure time scales are competing. In general, one of the most important questions about an evolving network is related to its synchronisation, that is, if the system will converge to a state in which all the nodes have the same behaviour. For example, by optimising the synchronisation of a multi-vehicles or mobile phones networks, it is possible to increase the efficiency of a certain function and reduce a cost. On the other hand, synchronised state in neural networks can be indicative of a brain disease, such as epilepsy.

Nonholonomic mechanics and its applications

Nonholonomic systems are a widespread topic in several scientific and commercial domains, including robotics, locomotion and space exploration. Roughly speaking, a nonholonomic constraint is a linear form in the virtual displacements of the system that cannot be integrated, that is it does not represent an integrable form. The equation of motion for a nonholonomic system can be obtained in two different ways. The first approach is to consider the Gauss principle of least and derive the so called Lagrange equations of the first kind for a nonholonomic systems. In this case, we obtain a system of Differential Algebraic Equations (DAEs) which allow to completely describe the free motion of the nonholonomic system. On the other hand, it is possible to use a variational principles suitably adapted for nonholonomic systems. However, there is a net difference if we apply the constraints before or after taking the variations. In the first case we have the so called Variational Nonholonomic Equations, which are suitable for optimal control, while in the latter we obtain the dynamic Lagrange-d'Alembert equation, which are the correct mechanical dynamical equations for the system. Both these methods lead to a system of Ordinary Differential Equations (ODEs) of the second order.

Nonlinear model for a bicycle

In the recent past, a great interest has been devoted towards bicycle modelling as it is a mechanical system characterized by nonholonomic constraints. Many researchers have tried to find proper equations to describe the dynamic of this system. Researchers usually derive the equation of motion either by using the Newton's laws or by studiing the system from a Lagrangian or Hamiltonian point of view. 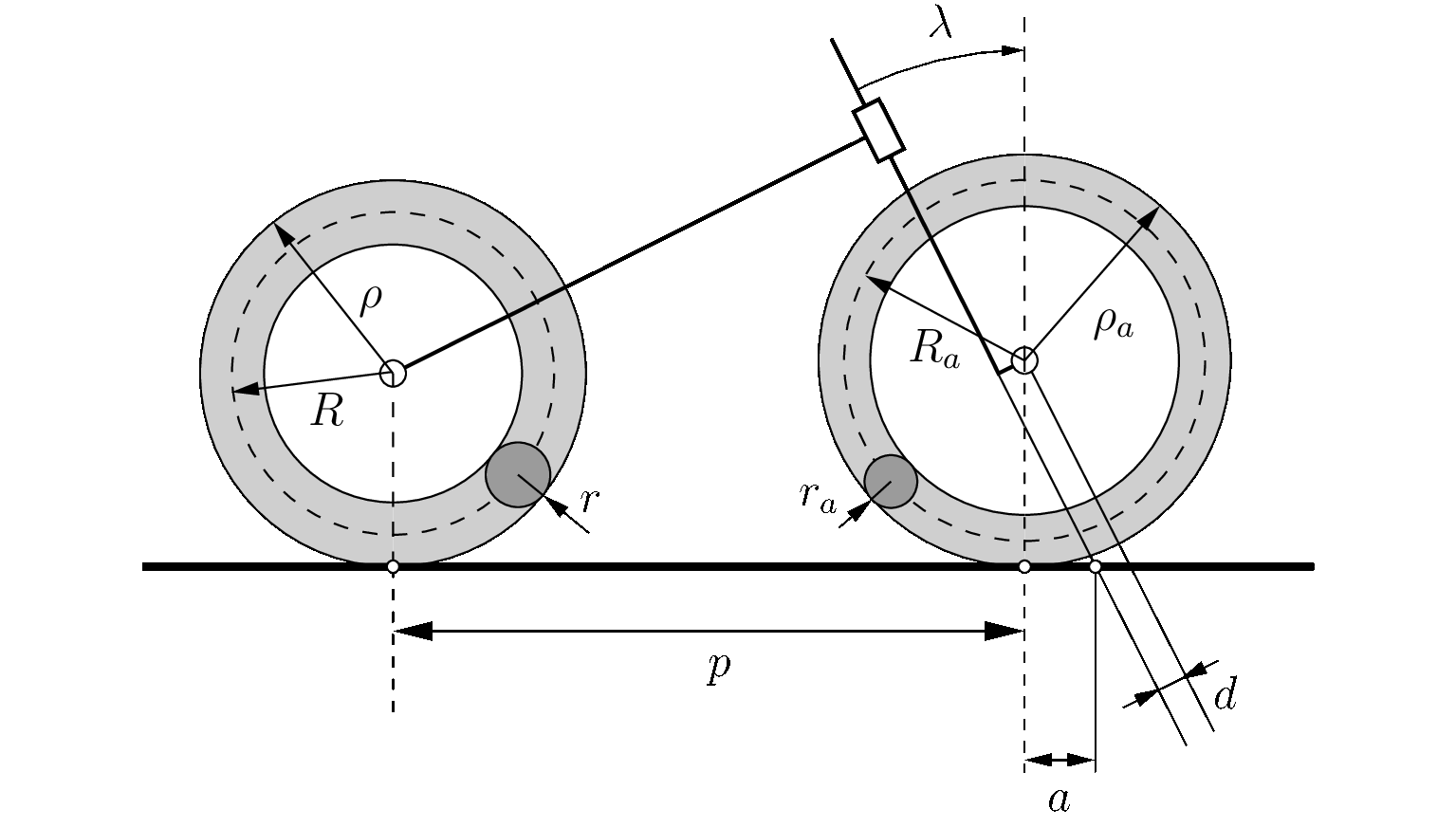So far, the greatest part of the existing literature has been devoted to models with lots of simplifications in order to describe a particular aspect of the bicycle's dynamic, and linearized equations of motion are commonly introduced in order to cope more easily with the problem. In contrast with this tendency to simplify the problem and study a linear model for the bicycle, I derive a nonlinear model of this system which considers a seven dimensional configuration space and accounts of the large number of geometric aspects that characterized a real bicycle. As shown in my thesis, the problem can be solved and the resulting equations of motion are a system of DAEs. This follows from the fact that the pitch angle is not constant and depends on some unknown Lagrangian coordinates. Therefore, when the equations of motion are numerically integrated, it is necessary to solve also an algebraic equation which gives the pitch angle.