BASE

Metodo Geometrico 

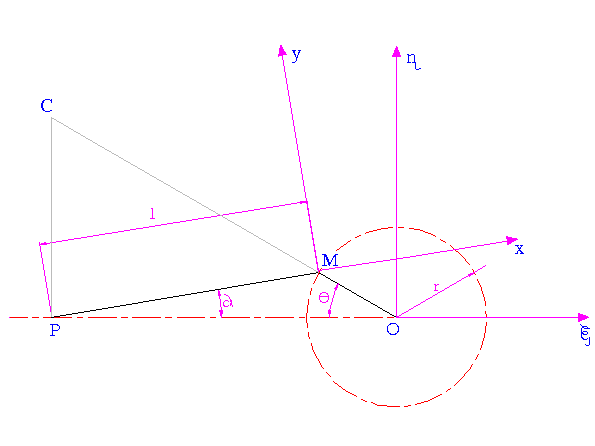
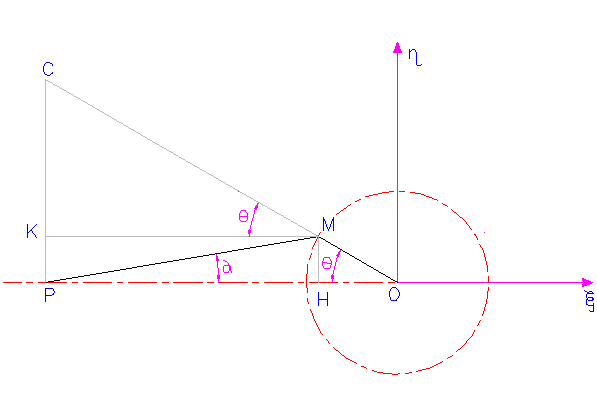
Nella risoluzione di problemi inerenti lo studio di Base e Rulletta  si utilizzino due sistemi di riferimento: uno “fisso“, rispetto al quale troviamo l’equazione della Base,  ed uno “mobile”, solidale con il sistema studiato rispetto al quale calcoliamo l’equazione della Rulletta.

Nel nostro caso, nello studio cioè del sistema costituito dalla Biella e dalla Manovella, va considerato come sistema di riferimento “fisso” una terna di coordinate destrorsa avente origine in O con asse delle ascisse orizzontale, asse delle ordinate verticale, i versi sono quelli indicati in Fig., ed asse delle quote ortogonale al foglio con verso uscente verso il lettore.

Come sistema di riferimento “mobile”, solidale con il movimento della biella, abbiamo considerato una terna di coordinate destrorsa avente origine coincidente con il piede di biella P, l’asse delle ascisse è diretto secondo l’asse della biella e l’asse delle ordinate è ortogonale a quello delle ascisse, i versi sono quelli indicati in Fig. , l’asse delle quote è ortogonale al piano del moto con verso individuato dalla “Regola della mano destra”.

Il sistema così individuato ha un solo grado di libertà : Si Individui con q la variabile del moto considerato (vedere Fig).

L'angolo q è quello che la manovella forma con l’orizzontale crescente in senso orario, con a, invece, quello che la biella forma con l’orizzontale, con l la lunghezza della Biella e con r quella della manovella.

Possiamo individuare la relazione trigonometrica che lega i due angoli a e q grazie al teorema dei seni:

PM cos a = OM sin q

cioè: 

l sin a = r sin q   

1
Quindi è possibile ricavare la seguente uguaglianza: 

a = [ arcsin  ( r sin q ) ] / l

2

Ora determiniamo due espressioni parametriche per individuare ascissa ed ordinata della Base.

Per quanto riguarda l’ascissa del centro di istantanea rotazione C consideriamo i due triangoli rettangoli OMH e PMH, con H piede della perpendicolare all’asse delle ascisse passante per M, vedere Fig.

utilizzando la trigonometria troviamo:

PO = PH + HO = PM cos a + OM cos q   

 cioè:  

xC = - ( r cos q + l cos a )  

mediante l’uso della ( 2 ) possiamo semplificare l’espressione ( 3 ) fino a portarla nella forma:

xC(q) = - r cos q - l cos { arcsin [ ( r sin q ) / l ] }

Per quanto riguarda l’ordinata del centro di istantanea rotazione consideriamo i triangoli rettangoli PHM e MHC, dove K è il piede della perpendicolare per M al segmento PC (vedere Fig. ).

Servendosi della trigonometria determiniamo l’ordinata del centro di istantanea  rotazione:

PC = PK + KC = OM sin q + KM tg q = OM sin q + PM cos a tg q    

 cioè:  

 hC =  r sin q + l tg q cos a
mediante l’uso della ( 2 ) otteniamo un’espressione in funzione solo di q:

hC(q) = r sin q + l ( cos ( ( arcsin ( r sin q ) ) / l ) tg q