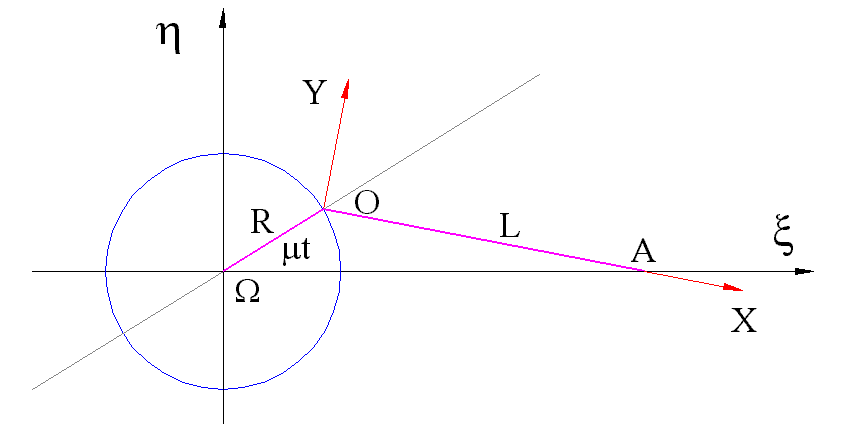
ANAtISI DEL MOTO RIGIDO DI UN MA NO VELLISMO DI SPINTA ORDINARIO

Possiamo così schematizzare il problema:

Indichiamo con AO una biella di lunghezza L e OW una manovella di lunghezza R che ruota uniformemente.

Il punto A dell’asta rigida di lunghezza L si muove sull’asse fisso Wx mentre il punto O dell’asta stessa descrive, di moto uniforme, la circonferenza x² + h² = R² on L > R (come in figura).

Sia m la velocità angolare costante della manovella e si assuma quale istante iniziale un istante in cui il punto O passa per il punto x = R, h = 0, è quindi lecito assumere uguale a mt l’angolo che ( O - W ) forma con Wx.

Per le ipotesi fatte il punto O ha coordinate

a = R cos mt

b = R sin mt

Le corrispondenti coordinate a₁ e b₁ del punto A sono

a₁ = R cos mt + ( L² - R² sin² mt ) ^1/2

b₁ = 0

Perciò la velocità del punto A ha le componenti secondo gli assi fissi:

a^'₁ = - R m sin mt - ( R² m sin mt cos mt ) / ( L² - R² sin² mt ) ^1/2

b^'₁= 0

Adesso cerchiamo l a velocit à angolare w della biella AO, la cui componente secondo k ci servirà per determinare le equazioni della base e della rulletta .

Assumiamo nel piano x h un sistema mobile con origine nel punto O, l'asse delle x parallelo ad (A - O) e con lo stesso verso, l'asse y normale ad (A - O) e costituente con l'asse delle x un sistema congruente agli assi x e h .

I terzi assi, perpendicolari al piano, z del sistema fisso, z del sistema mobile risultano paralleli e con lo stesso verso.

Sia j l'angolo che Ox fa con Wx , contato positivamente in senso antiorario per chi osserva la figura .

La velocità angolare W con la quale l'asta rigida ruota nel piano x h è chiaramente un vettore parallelo a z e quindi a z, avente secondo questi assi la componente j^' .

Perciò si ha :

w = j^'k

Per la determinazione di w basterà quindi determinare j^' . A questo scopo si nota che la biella si conosce il moto dei due punti A ed O. Dal teorema fondamentale della cinematica dei moti rigidi si ricava:ù

In cui si presenta come incognita w .

V_a - V_o = w _^ ( A-O ) = j^' _^ ( A-O )

Indichiamo con i_o e j_o i versori che individuano gli assi x ed h ; Il terzo asse z è individuato dallo stesso vettore k che individua l'asse mobile z.
Poichè :	A - O = ( a₁ -a ) i_{o -}b j_o
Allora, proittando l'equazione precedente sull'asse delle h si ottiene :	V_a - V_o = ( A' - O' ) = j^'( a₁ -a ) j_o+ j^'b i_o
Da cui	- b^'= j^'( a₁ -a )
E tenendo conto delle espressioni precedentemente determinati, si ha in definitiva	j^'= ( R m cos mt ) / ( L² - R² sin² mt )^1/2

L'equazione della base di un moto rigido piano

x_o = a - ( b^') / ( j^')

h_o = b + ( a^') / ( j^')

Per il moto della biella , in virtù delle ipotesi fatte diventano:

Queste equazione danno anche la legge del moto del centro istantaneo P_o sulla base stessa.

x_o= R cos mt + ( L² - R² sin² mt )^1/2

h_o = tg ( mt ( L² - R² sin² mt )^1/2) + R sen mt

La base simmetrica rispetto all’asse delle x, si compone di due rami che si estendono indefinitamente nel senso delle h positive e nel senso delle h negative ed aventi per asintoto comune la retta .

x = ( L² - R² )^1/2

Eliminando il tempo dall'equazione della Base si guinge all'equazione cartesiana della base del moto.

La base è quindi una sestica, cioè una curva algebrica del sesto ordine.

( x_o+h_o ) ( x_o²- L² + R² ) ² = R²x_o⁴

con x_o> L - R > 0