Università degli Studi di Firenze

Anno Accademico 2004/2005

Ingegneria per l'Ambiente e il Territorio

Corso di Analisi Matematica 2 (IAT)

Docente: prof.ssa Francesca Bucci

Periodo: III bimestre (21 febbraio 2005 - 16 aprile 2005)

Orario (indicativo): Mar.: 10:30-11:15, 11:30-12;15 (al termine, ricevimento studenti) - Gio.: 10:30-11:15, 11:30-12;15, 12:30-13;15. Spesso la lezione del martedì si protrarrà per 15 minuti, al fine di anticipare la conclusione della lezione del giovedì.

Lezioni svolte

A conclusione degli argomenti affrontati in ciascuna lezione, sono indicati (dentro una parentesi quadra) i paragrafi corrispondenti del testo di riferimento: R.A. ADAMS, Calcolo Differenziale 2 (Terza edizione), Casa Editrice Ambrosiana, Milano, 2003.

1. Mar. 22/2/05 - 2 ore

Presentazione del corso. Libro di testo e altri testi consigliati. Alcune informazioni pratiche.

Introduzione alle funzioni di due o più variabili. Lo spazio $\mathbb{R}^n$: definizioni di norma euclidea, e di distanza tra due punti. Definizione di intorno (sferico), insiemi limitati. Punti interni, esterni, di frontiera; insiemi aperti, chiusi. Punti di accumulazione. Primi esempi di funzioni di due o più variabili, a valori reali ( $f:D\subseteq \mathbb{R}^n\rightarrow \mathbb{R}$) e loro domini naturali. Grafici, curve di livello. Alcuni esempi: $f(x,y) = \sqrt{1-x^2-y^2}$, $g(x,y) = x^2+y^2$, ...

[C; 1.1, 1.2; 3.1]

2. Gio. 24/2/05 - 3 ore

Limiti e continuità. Sia $f:D\subseteq \mathbb{R}^n\rightarrow \mathbb{R}$, e sia $a$ una punto di accumulazione per $D$: definizione di limite finito di $f(x)$ per $x\to a$ (in termini di intorni). Il caso $n=2$, significato geometrico. Esempi e verifiche di limiti. Validità delle principali proprietà dei limiti note dal caso $n=1$ (unicità, permanenza del segno, regole di calcolo, etc.).

Definizione di funzione continua in un punto. Esempi. Alcune funzioni continue elementari: polinomi, funzioni razionali, potenze, etc. Continuità delle funzioni composte. Validità del TEOREMA DI WEIERSTRASS (s.d.). Insiemi connessi, validità del Teorema dei valori intermedi (s.d.).

Derivate parziali. Il problema di estendere al caso multidimensionale il concetto di funzione derivabile in un punto. Sia $f:D\subseteq \mathbb{R}^2\rightarrow \mathbb{R}$, e sia $(a,b)\in D$: definizione di derivata parziale di $f$ rispetto a $x$ in $(a,b)$ (simboli $f_x(a,b)$, $D_x(a,b)$, $D_1(a,b)$, $\frac{\partial f}{\partial x}(a,b)$). Analogamente per $f_y(a,b)$. Importante: una funzione $f$ che ammette entrambe le derivate parziali $f_x(a,b)$ e $f_y(a,b)$ può non essere continua in $(a,b)$. Esempi ed esercizi.

[3.2, 3.3]

ESERCIZI ASSEGNATI (I settimana): (§3.1) 8, 9, 14, 17, 22; (§3.2) 12, 14; (§3.3) 4, 6, 12.

3. Mar. 1/3/05 - 2 ore

Il problema di estendere il concetto di derivabilità a funzioni di più variabili: le derivate parziali non possono fornire l'estensione del concetto di derivata al caso di più variabili. Esistenza della derivata prima ed approssimazione lineare. Definizione di funzione differenziabile in un punto interno al dominio. Due conseguenze fondamentali: Sia $f$ una funzione differenziabile in un punto $(a,b)$: allora (i) $f$ è ivi continua; (ii) il grafico di $f$ ammette piano tangente in $(a,b,f(a,b))$. Equazione del piano tangente, direzione di un vettore normale al grafico di $f$ in $(a,b,f(a,b))$, equazione della retta normale. Una condizione sufficiente per la differenziabilità: Il Teorema del differenziale totale (s.d.). Funzioni di classe $C^1$. COROLLARIO: Se $f\in C^1(A)$, $f$ è differenziabile in $A$. Esercizio.

[3.6, 3.3]

4. Gio. 3/3/05 - 3 ore

Riepilogo delle definizioni e dei risultati principali introdotti nella lezione precedente. Il vettore gradiente. Definizione generale di funzione differenziabile in un punto (caso $n>2$). Alcuni esercizi su: piani tangenti, vettori normali, etc. Esercizio (n.34 del §3.3) sul calcolo della distanza di un punto da una superficie (si veda anche l'Esempio 8 del §3.3). Differenziale. Derivazione delle funzioni composte. Analisi dei casi $g(t):=f(u(t),v(t))$ e $g(u,v)= f(x(u,v),y(u,v))$. Ipotesi sulla regolarità delle funzioni e ``regola della catena'' (chain rule). Esempi: passaggio da coordinate cartesiane a coordinate polari; lo stesso per le coordinate sferiche (per eser.).

[3.6, 3.7, 3.5]

ESERCIZI ASSEGNATI (II settimana): (§3.3) 16, 22, 23; (§3.5) 14, Esempio 6; (§3.7) 2, 4, 6.

5. Mar. 8/3/05 - 2 ore

Un esempio di non validità della chain rule: il caso della funzione composta $g(t):=f(u(t),v(t))$, con

$$f(x,y)=\begin{cases} x & x=y\\ 0& x\ne y \end{cases}\,,$$

e $u(t)=v(t)=t$. Si effettua il calcolo di $g'(0)$ in due modi (di cui uno è errato).
Derivate di ordine superiore. Derivate seconde pure, miste. Il Teorema di Schwarz (s.d.). Funzioni di classe $C^2$. Definizione di funzione armonica; l'equazione di Laplace. Per esercizio: scrivere l'equazione di Laplace in coordinate polari. Esercizio 17 del §3.4 (equazione di diffusione del calore).
Direzioni in $\mathbb{R}^n$. Definizione di derivata direzionale di una funzione in un punto. TEOREMA: Sia $f$ una funzione differenziabile in un punto $p$ interno al dominio $D$ di $f$. Allora $f$ ammette derivate direzionali in $p$ lungo ogni direzione $v$ e si ha $\frac{\partial f}{\partial v}(p) = \nabla f(p)\cdot v$ per ogni $v$.
Direzioni di massima e minima pendenza del grafico di $f$. Esercizio: calcolo di derivate direzionali.

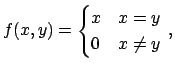
[3.5, 3.4, 3.7]

6. Gio. 10/3/05 - 3 ore

Sia $f\in C^2(D)$, $D\subseteq \mathbb{R}^2$, e sia $(a,b)$ un punto interno a $D$. Si introduce la Formula di Taylor di $f$, di ordine $2$, centrata in $(a,b)$, con resto di Lagrange. Si ricava da quella la Formula di Taylor di $f$, di ordine $2$, centrata in $(a,b)$, con resto di Peano. Usando una notazione vettoriale, con $p$ il punto fissato, $h$ l'incremento:

$$f(p+h)= f(p)+ \nabla f(p)\cdot h + \frac12 h^T\,H_f(p)\,h + o(\vert\vert h\vert\vert^2)\,, \quad h\to 0\,.$$

La matrice hessiana di $f$ ($H_f$). Applicazione al calcolo di limiti.

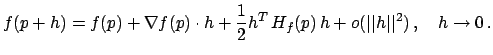
Valori estremi. Definizione di punto di massimo (o minimo) relativo. Punti di estremo (relativo ed assoluto). Esempi. TEOREMA (di Fermat): Sia $f:D\subseteq \mathbb{R}^n\to \mathbb{R}$, e sia $p$ un punto di estremo relativo per $f$ interno a $D$. Se $f$ è differenziabile in $p$, allora $\nabla f(p) = 0$ ($p$ è detto punto critico di $f$). Importante: il Teorema fornisce una condizione necessaria, ma non sufficiente a stabilire che un punto $p$--interno a $D$, su cui $f$ è differenziabile--sia effettivamente di estremo; esempio: $f(x,y)=x^2-y^2$ ($(0,0)$ non è di estremo per $f$).
Punti singolari (punti interni a $D$ in cui $f$ non è differenziabile). Punti critici, punti singolari, punti di frontiera. Due esercizi.

[3.9, 4.1]

7. Mar. 15/3/05 - 2 ore

Riepilogo delle nozioni e dei risultati principali introdotti nella lezione precedente: formule di Taylor di ordine $m$ con resto di Lagrange o di Peano, polinomio di Taylor; Teorema di Fermat (in relazione ai punti di estremo relativo). Attenzione: il Teorema di Fermat stabilisce una condizione solo necessaria affinché un punto (non singolare, interno a $D$) sia di estremo relativo per $f$. Punti critici che non sono di estremo.

Forme quadratiche: definizione ed esempi. Forme quadratiche definite positive, negative, semi-definite, indefinite. Criteri relativi: $(i)$ test sugli autovalori; $(ii)$ criterio di Jacobi (tramite i determinanti dei minori principali). Esempi. TEOREMA: condizioni ``del secondo ordine'' per la ricerca di punti di estremo relativo per funzioni $f\in C^2(D)$. Analisi della `definitezza' della matrice hessiana.

[1.6; 4.1, 4.2]

8. Gio. 17/3/05 - 3 ore

Risoluzione di alcuni problemi di massimo e/o minimo (tra cui: l'Esempio 9 del §4.2; il problema di determinare tre numeri positivi di somma data in modo che il loro prodotto sia massimo; il problema di determinare la distanza di un punto dello spazio dal grafico di una funzione di due variabili; etc.). Funzioni di tipo radiale su domini a simmetria radiale.

Funzioni a valori vettoriali: $f:D\subseteq \mathbb{R}^n\rightarrow \mathbb{R}^m$, $m>1$. Introduzione ed esempi: rappresentazioni parametriche di curve e superfici; campi vettoriali. Estensione al caso $m>1$ di concetti fondamentali quali quelli di limite, continuità, e differenziabilità. Matrice jacobiana.

[4.1, 4.2; 3.6]

9. Mar. 22/3/05 - 2 ore

Esercitazione relativa ai temi svolti fino alla data attuale (calcolo differenziale per funzioni di più variabili).

Funzioni a valori vettoriali (continuazione). Alcuni esercizi: la matrice jacobiana della trasformazione in coordinate polari; utilizzo della matrice jacobiana per il calcolo di valori approssimati di funzioni (Esercizi 13 e 15 del §3.6).
Il Teorema del valor medio (o di Lagrange) non vale, in generale, per funzioni a valori in $\mathbb{R}^m$, $m>1$: Esempio. Derivazione di funzioni composte. La regola della catena.

[3.6]

10. Gio. 24/3/05 - 3 ore

Integrazione multipla. Introduzione agli integrali doppi. Funzioni limitate su un rettangolo: partizioni e somme di Riemann. Proprietà degli integrali: linearità, monotonia, etc. Insiemi trascurabili. Teorema di integrabilità (s.d.). Teorema di Fubini (s.d.). Integrazione su domini semplici rispetto ad un asse.

[5.1, 5.2]

11. Mar. 5/4/05 - 2 ore

Cenni alla misura di Peano-Jordan. Applicazioni geometriche e fisiche degli integrali doppi: determinazione del baricentro di una lamina. Esercizi. Trasformazioni regolari e cambiamento di variabili negli integrali doppi. Coordinate polari.

[5.4, 5.7]

12. Gio. 7/4/05 - 3 ore

Esercizi sul cambiamento di variabili negli integrali doppi.
Integrali tripli. Cambiamento di variabili negli integrali tripli. Coordinate sferiche, coordinate cilindriche. Volume dei solidi di rotazione: il TEOREMA (DI PAPPO). Esempi.

[5.5, 5.6]

13. Mar. 12/4/05 - 2 ore

Esercizi sugli integrali tripli. Formule di riduzione: integrazione ``per fili'' e ``per strati''. Volume di un cono.

Curve in forma parametrica. Curve in forma cartesiana e in forma parametrica. Esempi. Curve polari. Curve regolari. Cambi di parametro ammissibili, parametrizzazioni equivalenti. Curve rettificabili: lunghezza di una curva. Teorema di rappresentazione per la lunghezza di un arco di curva regolare (s.d.). La lunghezza non dipende dalla parametrizzazione scelta (s.d.).

[5.5, 5.6; 2.3, 6.3]

14. Gio. 14/4/05 - 3 ore

Curve in forma parametrica (continuazione). Il parametro lunghezza d'arco (o ascissa curvilinea): rappresentazione standard. Esempio.
Curve regolari a tratti. Integrali di linea sul sostegno di un arco di curva regolare, o regolare a tratti. Calcolo del baricentro di un filo.

Curve in forma implicita. L'assunto del TEOREMA DELLE FUNZIONI IMPLICITE (o del Dini) per l'insieme $Z$ descritto dall'equazione $F(x,y)=k$, con $F\in C^1$: Se $(x_0,y_0)\in Z$, e $\nabla F(x_0,y_0)\neq 0$, allora $Z$ è localmente (in un intorno di $(x_0,y_0)$) il grafico di una funzione di una variabile $x\mapsto y(x)$ o $y\mapsto x(y)$. Conseguenza importante: se $\nabla F(x_0,y_0)\neq 0$, $\nabla F(x_0,y_0)$ è un vettore ortogonale, in $(x_0,y_0)$, all'insieme descritto da $F(x,y)=k$.

Superfici in forma parametrica (molto rapidamente). Superfici cartesiane. Superfici regolari. Linee coordinate. Piano tangente ad una superficie in un punto. Versore normale. Area di una superficie regolare. Integrali di superficie.

[6.3; 6.5]

15. (Lezione integrativa) Ven. 15/4/05 - 2 ore

Esercizi e problemi relativi al calcolo di volumi, e in generale di integrali tripli; curve e superfici regolari.