Anno Accademico 2002-2003

Università degli Studi di Firenze

Ingegneria per l'Ambiente e il Territorio

Corso di Analisi Matematica II

Periodo: 25 novembre 2002 - 25 gennaio 2003.

Docente: prof.ssa Francesca Bucci.

Lezioni svolte

I capitoli, le sezioni o le pagine indicate al termine delle lezioni si riferiscono al testo di riferimento: R.A. ADAMS, Calcolo Differenziale 1 (Seconda edizione), Casa Editrice Ambrosiana, Milano, 1999.

1. Gio. 28/11/02 - 3 ore

Il tema iniziale del corso si riallaccia al programma del corso Analisi Matematica I. In particolare, si prosegue sul tema `Applicazioni del Teorema del valor medio'. Il teorema del valor medio generalizzato (s.d.). Approssimazione di funzioni: approssimazioni lineari, quadratiche. Formula di Taylor con resto di Lagrange (dimostrata la formula di ordine $1$ utilizzando il teorema del valor medio generalizzato). Polinomi di Taylor. Funzioni con derivate di ordine arbitrario. Calcolo dei polinomi di Taylor di ordine $n$ delle funzioni $e^x$, $\sin x$.

Applicazione della formula di Taylor con resto di Lagrange al calcolo approssimato di numeri. Calcolo di un valore approssimato di $\sqrt{e}$ con due cifre decimali corrette. Per esercizio: calcolo di un valore approssimato di $\sqrt[3]{e}$.

[5.1, 5.6]

2. Ven. 29/11/02 - 2 ore (dott.ssa R. CAVAZZONI)

Polinomio di Taylor della funzione $\cos x$, di ordine $n$, con centro in $0$. Sviluppi delle funzioni: $\frac1{1-x}$, $\frac1{1+x}$, $\frac1{1+x^2}$.

Formula di Taylor con resto di Peano. (Attenzione: la formula di Taylor con resto di Peano non è trattata nel testo di riferimento). Il simbolo di Landau o piccolo: significato della notazione $f(x) = o(g(x))$, $x\to a$. Applicazione al calcolo di limiti. Esercizio: calcolo del limite $\lim_{x\to 0} \frac{x-sin x}{x^3}$.

Definizione: $f(x)^{g(x)}$, con $f(x) >0$, significa $e^{g(x) \log f(x)}$. Esercizio: provare (senza calcolatrice) che $e^\pi>\pi^e$.

Le funzioni coseno e seno iperbolico ($\cosh x$ e $\sinh x$, rispettivamente).

[5.6, 4.6]

3. Gio. 5/12/02 - 3 ore

Richiamo della formula di Taylor con resto di Peano. Esercizi: sviluppi di alcune funzioni; applicazione al calcolo di limiti. Forme indeterminate e regole di de l'Hôpital: primo e secondo teorema di de l'Hôpital. Esercizi. Confronto tra diversi metodi per il calcolo dei limiti. Richiamo dei limiti notevoli $\lim_{t\to 0} \frac{\sin t}{t}=1$, $\lim_{t\to 0} \frac{1-\cos t}{t^2}=\frac12$. I limiti notevoli $\lim_{t\to 0}\frac{e^t - 1}{t}=1$, $\lim_{t\to 0}\frac{a^t - 1}{t}=\log a$, $a>0$, come conseguenza del fatto $De^t= e^t$.

Somme e simbolo di sommatoria. Esempi di somme con la notazione di sommatoria. Calcolo di alcune somme:

$$\sum_{k=1}^n k= \frac{n(n+1)}2\,, \quad \sum_{k=1}^n k^2= \... ... \quad \sum_{k=0}^n x^k = \frac {1-x^{n+1}}{1-x}\,,x\ne 1\,.$$

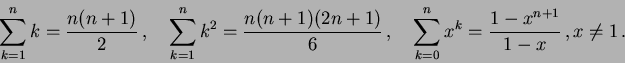
[5.5; 6.1]

4. Ven. 6/12/02 - 2 ore (dott.ssa R. CAVAZZONI)

Aree come limiti di somme. Esempi: calcolo dell'area delle figure delimitate dai grafici delle funzioni $y=x$, $x\in [0,2]$ e $y=x^2$, $x\in [0,b]$ (v. Esempi 1-2, § 6.2). Partizioni e somme di Riemann. Somme superiori e inferiori per funzioni continue in un intervallo $[a,b]$: definizione di integrale definito. Assegnati $5$ esercizi dei paragrafi $6.2$ e $6.3$.

[6.2,6.3]

5. Gio. 12/12/02 - 3 ore

Lezione sospesa (su indicazione del Preside, per permettere la partecipazione alle assemblee di studenti e personale).

6. Ven. 13/12/02 - 2 ore

Lezione sospesa (occupazione studentesca).

7. Gio. 19/12/02 - 3 ore

Integrale secondo Riemann (continua). Somme di Riemann generali. L'integrale come limite di somme di Riemann. Proprietà dell'integrale definito.

PROPOSIZIONE: Le funzioni continue su un intervallo chiuso e limitato $[a,b]$ sono integrabili (s.d.). Estensione della definizione di integrale (definito) ed altre classi di funzioni integrabili in $[a,b]$ (s.d.): funzioni monotòne e limitate in $[a,b]$; funzioni continue a tratti (o a pezzi).

Primitive e integrali indefiniti. Esempi. Teorema della media integrale. Funzioni integrali. TEOREMA FONDAMENTALE DEL CALCOLO INTEGRALE (con dim.).

[6.3, 6.4, 6.5]

8. Ven. 20/12/02 - 2 ore

Applicazione del Teorema fondamentale del calcolo integrale. ESERCIZI: derivazione di funzioni composte da funzioni integrali; es. 57, § 6.5.

Una tabella di integrali indefiniti. Funzioni elementari le cui primitive non sono esprimibili mediante funzioni elementari (e.g., $\int e^{-t^2} {\rm d}t$). Tecniche di integrazione. Il metodo di sostituzione. Integrazione di funzioni razionali $\frac{P(x)}{Q(x)}$, con $P(x)$ e $Q(x)$ polinomi: richiami sulla divisione di polinomi, riduzione al caso in cui il grado del numeratore $P(x)$ è inferiore al grado del denominatore $Q(x)$. Analisi del caso in cui $Q(x)$ è un trinomio di secondo grado. Decomposizione delle funzioni razionali in frazioni semplici.

[6.6, 7.3]

9. Mer. 8/1/03 - 2 ore (Lezione di recupero)

Discussione di alcuni esercizi assegnati per il periodo natalizio.

Decomposizione delle funzioni razionali (continua). Analisi del caso in cui il denominatore $Q(x)$ ha grado due: $Q(x)$ con due radici reali, $Q(x)$ con una radice di molteplicità due, $Q(x)$ irriducibile; esempi. Il caso in cui il denominatore $Q(x)$ ha grado tre; esempi.

[7.3]

10. Gio. 9/1/03 - 3 ore

Tecniche di integrazione. Integrazione per parti; esempi. Gli integrali $\int \cos^2 x\,dx$, $\int \sin^2 x\,dx$. Uso dell'integrazione per parti per ottenere formule di riduzione (e dunque successioni definite per ricorrenza). Calcolo di $I_n=\int_0^{\pi/2} \sin^n x\,dx$ (introduzione del fattoriale doppio $n!!$).

Integrazione per sostituzione. Sostituzioni ammissibili, formula di integrazione per sostituzione. Integrali $\int \phi(\sqrt{a^2 - x^2})\,dx$, $\int \phi(\sqrt{a^2 + x^2})\,dx$, $\int \phi(\sqrt{x^2 - a^2})\,dx$: le sostituzioni trigonometriche $x= a\sin t$, $x= a\tan t$ (oppure $x= a\sinh t$), $x= a\sec t$ (oppure $x= a\cosh t$). Esempi. La sostituzione $x=\tan(\theta/2)$.

[7.1, 7.2]

11. Ven. 10/1/03 - 2 ore (dott.ssa R. CAVAZZONI)

Esercizi conclusivi sulle varie tecniche di integrazione (§ 7: n. 17, 29, 73, 76, 79, p. 419). Calcolo di aree di regioni piane. Esempi. § 6.7: n. 10 (n. 21 lasciato per esercizio).

12. Gio. 16/1/03 - 3 ore

INTEGRALI IMPROPRI. Integrali impropri di primo tipo (l'insieme di integrazione non è limitato). Definizione di funzione $f$ integrabile in senso improprio in $[a,+\infty)$ (o in $(-\infty,b]$). Integrali convergenti, integrali divergenti. Esempi. Analisi della convergenza dell'integrale $\int_1^{\infty} \frac{1}{x^p}\, dx$, al variare del parametro $p$ (converge se e solo se $p>1$).

Integrali impropri di secondo tipo (la funzione integranda non è limitata in un intorno di un punto). Definizione di integrabilità in senso improprio in $(a,b)$ per una funzione $f$ illimitata vicino ad $a$ (o vicino a $b$). Integrali convergenti, divergenti. Esempi. Analisi della convergenza dell'integrale $\int_0^1 \frac{1}{x^p}\, dx$ al variare del parametro $p$ (converge se e solo se $p<1$).

Determinazione della convergenza o divergenza di un integrale improprio: Teorema: Il criterio del confronto (s.d.). Esempi. Convergenza dell'integrale $\int_0^\infty e^{-t^2}\, dt$ mediante il criterio del confronto. (Importante: $\int_0^\infty e^{-t^2}\, dt= \frac{\sqrt{\pi}}2$).

[7.5]

13. Ven. 17/1/03 - 2 ore (dott.ssa R. CAVAZZONI)

EQUAZIONI DIFFERENZIALI ORDINARIE (EDO). Primi esempi di EDO del primo ordine: equazione della crescita e del decadimento. Equazione logistica. Equazioni a variabili separabili. Definizione di soluzione. Risoluzione di EDO a variabili separabili. L'equazione logistica come equazione a variabili separabili. Altri esempi; soluzioni di $y'=y^2$. Definizione di soluzione di un problema ai valori iniziali. Esempio 2 p. 484.

EDO lineari del primo ordine (a coefficienti continui). Integrale generale dell'equazione, soluzione dei corrispondenti problemi ai valori iniziali. Esercizio 16 p. 489.

Assegnati gli esempi 3, 4, 5 p. 484 e gli esercizi 3, 6, 10, 11, 14, 15, 18, 19, 21 p. 489.

[4.4, 8.9]

14. Mar. 21/1/03 - 1 ora (Lezione per il corso di Fisica Generale I; tema della lezione condiviso)

NUMERI COMPLESSI E FUNZIONI ESPONENZIALI COMPLESSE. Richiami preliminari (dal corso di Geometria): forma algebrica dei numeri complessi, aritmetica complessa. Rappresentazione geometrica dei numeri complessi (diagramma di Argand), il piano di Gauss. Forma trigonometrica (o polare) di un numero complesso: modulo, argomento, argomento principale.

Operazioni di prodotto, divisione ed elevamento a potenza: Teorema di de Moivre. Definizione dell'esponenziale $e^{i\theta}$, $\theta \in \mathbb{R}$: $e^{i\theta} = \cos \theta + i \sin \theta$ (formula di Eulero). Esempi sul calcolo di potenze di numeri complessi. Radici di un numero complesso (cenni); esempi.

Funzioni di variabile complessa (a valori complessi). Definizione della funzione esponenziale $e^z$, $z\in \mathbb{C}$. Continuità e derivabilità per funzioni complesse. Un caso importante: funzioni di variabile reale a valori complessi. Derivata della funzione $t\rightarrow e^{i\omega t}$.

[Appendici I e II]

15. Gio. 23/1/03 - 3 ore

EDO (continua). L'equazione del primo ordine $x' = f(t,x)$: definizione di soluzione. EDO a variabili separabili; esempi. Il caso lineare: l'equazione $x' = a(t)x + b(t)$, con $a$, $b\in C(I)$, $I\subseteq \mathbb{R}$. Determinazione dell'integrale generale, problema di Cauchy (o ai valori iniziali) associato e unicità della soluzione corrispondente.

EDO nonlineari. Soluzioni locali e soluzioni globali. Esempio di blow up (scoppiamento in tempo finito): soluzione del problema $x'= x^2$, $x(0)=1$.

EDO lineari del secondo ordine a coefficienti costanti. Analisi dell'equazione omogenea $ax'' + b x' + cx =0$: l'equazione (algebrica) ausiliaria $az^2 + b z + c =0$. Radici e soluzioni linearmente indipendenti (sistema fondamentale di soluzioni). Determinazione dell'integrale generale come combinazione lineare di soluzioni linearmente indipendenti. Esercizi.

[8.9, 4.7]

16. Ven. 24/1/03 - 2 ore (Lezione conclusiva del corso)

EDO lineari del secondo ordine: l'equazione non omogenea $a x'' + b x' + c x = f(t)$, $a$, $b$, $c$ costanti, $f\in C(I)$, $I\subseteq \mathbb{R}$. Integrale generale dell'equazione come somma dell'integrale generale dell'equazione omogenea associata e di una soluzione particolare dell'equazione non omogenea. Il problema della ricerca di una soluzione particolare. Analisi del caso in cui $f(t) = P_m(t) e^{\mu t}$, $P_m(t)$ polinomio di grado $m$, $\mu\in \mathbb{C}$: il metodo dei coefficienti indeterminati. Esempi ed esercizi.

[Calcolo Differenziale 2, Cap. 8]