Università degli Studi di Firenze
Ingegneria per l'Ambiente e il Territorio
Corso di Analisi Matematica I
Periodo: 23 settembre - 9 novembre 2002.
Docente: prof.ssa Francesca Bucci.
I capitoli, le sezioni o le pagine indicate al termine delle
lezioni si riferiscono al testo di riferimento:
R.A. ADAMS, Calcolo Differenziale 1
(Seconda edizione), Casa Editrice Ambrosiana, Milano, 1999.
1. Mar. 24/9/02 - 2 ore
Presentazione del corso. Libro di testo e altri testi consigliati. Alcune informazioni pratiche.
PRELIMINARI. Numeri reali e retta reale. Proprietà algebriche, d'ordine e di completezza dei numeri reali. Numeri interi e numeri razionali. Intervalli. L'unione e l'intersezione insiemistica.
[P.1]
2. Gio. 26/9/02 - 2 ore
Il valore assoluto: definizione e proprietà.
La disuguaglianza triangolare (con dim.). Esempi.
Equazioni e disequazioni con valori assoluti.
La radice quadrata di un numero positivo.
Importante:
![]() .
.
Coordinate cartesiane nel piano. Incrementi e distanze. Linee rette. Equazioni delle rette. Equazioni quadratiche. Circonferenze, parabole, ellissi, iperboli. Completamento del quadrato.
Funzioni.
[P.1-2-3-4]
3. Ven. 27/9/02 - 3 ore
Alcune precisazioni/aggiunte sui temi delle lezioni precedenti:
Funzioni. Dominio, codominio, immagine. Esempi. Grafico di una funzione.
Grafici di alcune funzioni elementari (![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ).
Funzioni pari, dispari e proprietà di simmetria dei relativi grafici.
La funzione parte intera:
).
Funzioni pari, dispari e proprietà di simmetria dei relativi grafici.
La funzione parte intera: ![]() .
Grafici ottenuti da grafici di funzioni elementari tramite
traslazioni e/o riflessioni. Funzioni razionali (rapporto di polinomi).
.
Grafici ottenuti da grafici di funzioni elementari tramite
traslazioni e/o riflessioni. Funzioni razionali (rapporto di polinomi).
(Richiamo: l'operazione di divisione tra polinomi).
Operazioni tra funzioni. Composizione di funzioni. Esempi.
[P.4-5]
4. Mar. 1/10/02 - 2 ore
Funzioni trigonometriche.
Lunghezza d'arco, misura degli angoli in radianti.
Seno e coseno. Proprietà fondamentali
(ad es.,
![]()
![]() ;
n.b.:
;
n.b.: ![]() significa
significa ![]() ).
Periodicità delle funzioni circolari.
Funzioni periodiche, periodo minimo; esempi.
Coseno e seno di angoli particolari (ad es.,
).
Periodicità delle funzioni circolari.
Funzioni periodiche, periodo minimo; esempi.
Coseno e seno di angoli particolari (ad es., ![]() ,
, ![]() ,
, ![]() ,
etc.).
Grafici delle funzioni
,
etc.).
Grafici delle funzioni ![]() e
e ![]() .
Formule di addizione.
Altre funzioni trigonometriche (in particolare, la tangente).
.
Formule di addizione.
Altre funzioni trigonometriche (in particolare, la tangente).
[P.6]
Introduzione ai LIMITI. Esempio: l'area di un cerchio come ``limite'' dell'area di poligoni regolari inscritti.
[1.1]
5. Gio. 3/10/02 - 2 ore (dott.ssa R. CAVAZZONI)
Limiti delle funzioni. Definizione informale, esempi.
Definizione formale di limite. Alcuni limiti elementari.
Limiti destro e sinistro. La funzione ![]() .
Regole per il calcolo dei limiti. Esempi.
Teorema dei carabinieri.
Esercizi.
.
Regole per il calcolo dei limiti. Esempi.
Teorema dei carabinieri.
Esercizi.
[1.2, 1.5]
6. Ven. 4/10/02 - 3 ore
Richiami dalla precedente lezione: la definizione di limite (finito),
uso della definizione per dimostrare che ![]() per
per ![]() .
Esercizi sui limiti: limiti di quozienti (esercizi 1.2: n. 31, 40);
il limite
.
Esercizi sui limiti: limiti di quozienti (esercizi 1.2: n. 31, 40);
il limite
![]() per
per ![]() (n. 95);
limiti di funzioni definite a tratti (n. 75-78).
(n. 95);
limiti di funzioni definite a tratti (n. 75-78).
Limiti all'infinito: esempi e definizione formale.
Limiti all'infinito per funzioni razionali:
discussione di
![]() al variare dei gradi
al variare dei gradi ![]() ,
, ![]() di
di ![]() e
e ![]() , rispettivamente.
Definizione di
, rispettivamente.
Definizione di
![]() .
.
[1.5, 1.2, 1.3]
7. Mar. 8/10/02 - 2 ore
Esercizi su limiti all'infinito.
(ad esempio, i n. ![]() ,
, ![]() della sezione 1.3).
Limiti infiniti. La funzione
della sezione 1.3).
Limiti infiniti. La funzione
![]() ,
, ![]() .
Esempi ed esercizi.
Asintoti orizzontali e verticali.
.
Esempi ed esercizi.
Asintoti orizzontali e verticali.
[1.3]
8. Gio. 10/10/02 - 3 ore
Funzioni continue. Punti interni al dominio di una funzione,
punti di frontiera. Esempi. Definizione di continuità in un punto.
Continuità in un intervallo.
Classi di funzioni continue: polinomi, funzioni razionali, potenze
razionali (![]() ), funzioni trigonometriche (seno, coseno,
tangente, secante, etc.), la funzione valore assoluto.
), funzioni trigonometriche (seno, coseno,
tangente, secante, etc.), la funzione valore assoluto.
Combinazione di funzioni continue (somma, prodotto, ...). TEOREMA: La composizione di funzioni continue è una funzione continua (s.d.). Discontiuità rimovibili ed estensioni continue. Esempi.
Proprietà delle funzioni continue.
IL TEOREMA DI WIERSTRASS: Una funzione continua in un intervallo
chiuso e limitato ammette valori massimo e minimo assoluti.
Formulazione matematica di problemi di massimo/minimo:
esecizio ![]() , sez. 1.4.
, sez. 1.4.
[1.4]
9. Ven. 11/10/02 - 2 ore (dott.ssa R. CAVAZZONI)
Proprietà delle funzioni continue (prosegue dalla lezione precedente). Il Teorema dei valori intermedi: applicazione alla ricerca della radici di equazioni. Il metodo di bisezione (cenni). Permanenza del segno.
Esercizi ![]() ,
, ![]() ,
, ![]() ,
, ![]() (sez. 1.4); es.
(sez. 1.4); es. ![]() (sez. 1.5).
(sez. 1.5).
[1.4, 1.5]
10. Mar. 15/10/02 - 2 ore
Introduzione al concetto di DERIVATA.
La retta tangente al grafico di una funzione ![]() in un punto
in un punto ![]() come ``limite'' di rette secanti.
Esempi: le curve di equazione
come ``limite'' di rette secanti.
Esempi: le curve di equazione ![]() ,
, ![]() ,
,
![]() ,
, ![]() . Punti cuspidali e punti angolosi, rette di
appoggio. Rette normali.
Rapporto incrementale e definizione di derivabilità di una funzione
. Punti cuspidali e punti angolosi, rette di
appoggio. Rette normali.
Rapporto incrementale e definizione di derivabilità di una funzione ![]() in un punto
in un punto ![]() interno al dominio.
Derivate destra e sinistra (
interno al dominio.
Derivate destra e sinistra (![]() e
e ![]() ).
La funzione derivata (prima)
).
La funzione derivata (prima)
![]() .
.
Derivate di alcune funzioni elementari (![]() ,
, ![]() , con
, con ![]() ,
,
![]() ,
, ![]() , ...).
, ...).
[2.1, 2.2]
11. Gio. 17/10/02 - 3 ore
Esercitazione: risoluzione di alcuni problemi con consegna degli elaborati (temi: limiti, continuità, rette tangenti e derivate).
Regole di derivazione. Derivate di funzioni ottenute tramite somma, moltiplicazione per una costante, prodotto, reciproco, quoziente. Esempi. Derivazione di funzioni composte (Teorema): la ``regola della catena''. Esempi.
[2.2, 2.3, 2.5]
12. Ven. 18/10/02 - 2 ore
Lezione sospesa causa sciopero.
13. Mar. 22/10/02 - 2 ore
Svolgimento dei primi due problemi dell'esercitazione del 17/10/02 e commenti sugli elaborati.
Il limite notevole
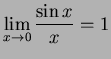 (dimostrato).
Derivate delle funzioni
(dimostrato).
Derivate delle funzioni ![]() e
e ![]() .
.
[2.4]
14. Gio. 24/10/02 - 3 ore
Derivate delle funzioni trigonometriche (![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ).
Esercizi di calcolo.
Il limite notevole
).
Esercizi di calcolo.
Il limite notevole
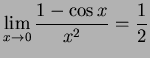 (dimostrato).
(dimostrato).
Derivate di ordine superiore.
Esempio: la funzione
![]() verifica
verifica
![]() per ogni
per ogni ![]() .
L'equazione (differenziale) dell'oscillatore armonico (§ 3.1).
Funzioni con derivate di ogni ordine.
.
L'equazione (differenziale) dell'oscillatore armonico (§ 3.1).
Funzioni con derivate di ogni ordine.
Un esempio sull'uso della derivazione implicita (§ 2.8, es. 2).
Svolgimento degli ultimi due problemi dell'esercitazione del 17/10/02 e commenti sugli elaborati.
[2.4, 2.7, 2.8, 3.1]
15. Ven. 25/10/02 - 2 ore (dott.ssa R. CAVAZZONI)
Rapidità di variazione media e istantanea: definizioni ed esercizio n. 27, § 2.6.
Regola generale della derivata di una potenza (tramite derivazione implicita).
Variazioni collegate: esempio ![]() p. 172 (pallone sferico).
p. 172 (pallone sferico).
Valori estremi: massimi e minimi assoluti e relativi (o locali). TEOREMA DI FERMAT: Sia
[2.6, 2.8; 3.2, 3.3]
16. Mar. 29/10/02 - 2 ore
Valori estremi di una funzione continua su un intervallo ![]() chiuso e limitato: richiami ai teoremi di Weierstrass (esistenza
dei valori estremi e dei punti di estremo) e di Fermat (punti critici
e localizzazione dei punti di estremo).
chiuso e limitato: richiami ai teoremi di Weierstrass (esistenza
dei valori estremi e dei punti di estremo) e di Fermat (punti critici
e localizzazione dei punti di estremo).
Immagini di funzioni continue in un intervallo. Esempi.
Funzioni continue su un intervallo non chiuso e/o non limitato.
Applicazione del Teorema di Weierstrass:
esistenza del valore minimo di funzioni continue che tendono a ![]() per
per ![]() e per
e per ![]() .
Esempio: ricerca delle dimensioni di un oggetto di forma cilindrica
che rendono minima la superficie, fissato il volume (§ 3.4, Esempio 5).
.
Esempio: ricerca delle dimensioni di un oggetto di forma cilindrica
che rendono minima la superficie, fissato il volume (§ 3.4, Esempio 5).
Il TEOREMA DEL VALOR MEDIO (O DI LAGRANGE); il Teorema di Rolle (dimostrati). Interpretazione geometrica. Esercizio.
[3.3, 3.4, 5.1]
17. Gio. 31/10/02 - 3 ore
Applicazioni del Teorema del valore medio. Funzioni con derivata nulla in un intervallo. Esempi.
Funzioni (monotòne) crescenti e decrescenti.
Teorema: Sia ![]() funzione continua in
funzione continua in ![]() e derivabile in
e derivabile in ![]() .
Allora
(i)
.
Allora
(i) ![]() è crescente (decrescente) in
è crescente (decrescente) in ![]() se e solo se
se e solo se
![]() (
(![]() ) per ogni
) per ogni ![]() ; (ii) se
; (ii) se
![]() (
(![]() ) per ogni
) per ogni ![]() , allora
, allora
![]() è strettamente crescente (decrescente) in
è strettamente crescente (decrescente) in ![]() .
.
Studio degli intervalli di monotonia di una funzione ![]() mediante
studio del segno della derivata prima
mediante
studio del segno della derivata prima ![]() , e disegno di un
grafico qualitativo. Esempio:
, e disegno di un
grafico qualitativo. Esempio:
![]() .
.
Applicazione: disuguaglianze tra funzioni su un intervallo. Esercizio 55.
[5.1, 5.2]
18. Mar. 5/11/02 - 2 ore
Richiamo del Teorema discusso nella lezione precedente.
Osservazione: Il viceversa del punto (ii) è in generale falso.
Infatti, una funzione ![]() derivabile in
derivabile in ![]() ,
strettamente monotòna in
,
strettamente monotòna in ![]() , può avere derivata nulla.
Esempio:
, può avere derivata nulla.
Esempio: ![]() .
.
Ricerca delle radici reali di un polinomio, o di zeri di una generica funzione continua. Esempi ed esercizi.
Insiemi convessi nel piano. Esempi.
Definizione di funzione convessa in ![]() .
(Attenzione: la definizione data è quella più usuale, valida per
funzioni di una o più variabili, ed è diversa da quella del libro di
testo, che è da noi in seguito ricavata come proprietà delle funzioni
convesse derivabili in
.
(Attenzione: la definizione data è quella più usuale, valida per
funzioni di una o più variabili, ed è diversa da quella del libro di
testo, che è da noi in seguito ricavata come proprietà delle funzioni
convesse derivabili in ![]() ).
Interpretazione geometrica. Esempi.
L'epigrafico
).
Interpretazione geometrica. Esempi.
L'epigrafico ![]() .
Caratterizzazione delle funzioni convesse derivabili in
.
Caratterizzazione delle funzioni convesse derivabili in ![]() :
PROPOSIZIONE:
Le proprietà seguenti sono equivalenti: (i)
:
PROPOSIZIONE:
Le proprietà seguenti sono equivalenti: (i) ![]() è convessa in
è convessa in
![]() ; (ii)
; (ii) ![]() è una funzione crescente in
è una funzione crescente in ![]() ;
(iii) per ogni
;
(iii) per ogni ![]() in
in ![]() si ha
si ha
![]() (cioé il grafico di
(cioé il grafico di ![]() ``sta sopra'' le sue rette tangenti).
``sta sopra'' le sue rette tangenti).
Funzioni ![]() con derivata seconda
con derivata seconda ![]() ,
, ![]() .
Studio del segno della derivata seonda per la determinazione degli intervalli
in cui
.
Studio del segno della derivata seonda per la determinazione degli intervalli
in cui ![]() è convessa (o concava).
Esempi.
Punti di flesso.
è convessa (o concava).
Esempi.
Punti di flesso.
[5.3]
19. Mar. 5/11/02 - 2 ore (recupero) (dott.ssa R. CAVAZZONI)
Studio dei grafici di funzioni. Applicazioni (ad esempio: validità di disuguaglianze). Esercizi.
[5.2, 5.3, 5.4]
20. Gio. 7/11/02 - 3 ore
Funzioni iniettive, funzioni suriettive. Esempi. Funzioni biunivoche. Esempi. Funzione inversa. Identità di cancellazione. Grafici di funzioni inverse. Funzioni inverse derivabili: formula per il calcolo della derivata della funzione inversa.
Funzioni trigonometriche inverse. Funzione arcoseno (![]() ),
funzione arcotangente (
),
funzione arcotangente (![]() ). Proprietà principali, grafici.
Calcolo delle derivate.
Esercizio: provare l'identità
). Proprietà principali, grafici.
Calcolo delle derivate.
Esercizio: provare l'identità
![]() ,
, ![]() .
Funzione arcocoseno (per esercizio).
.
Funzione arcocoseno (per esercizio).
[4.1, 4.5]
21. Ven. 8/11/02 - 2 ore (dott.ssa R. CAVAZZONI)
Funzioni trascendenti: le funzioni logaritmo ed esponenziale.
Introduzione al logaritmo naturale per via geometrica:
il grafico della funzione ![]() ,
, ![]() , e
definizione della funzione
, e
definizione della funzione ![]() tramite l'area di una opportuna
regione piana (§ 4.3).
PROPOSIZIONE: La funzione
tramite l'area di una opportuna
regione piana (§ 4.3).
PROPOSIZIONE: La funzione ![]() è derivabile,
e
è derivabile,
e
![]() ,
, ![]() .
.
La funzione ![]() come funzione inversa di
come funzione inversa di ![]() .
Il numero
.
Il numero ![]() .
Esercizio 28 (§ 4.3).
Crescita e decadimento delle funzioni esponenziale esponenziale e logaritmo.
Comportamento asintotico e confronto tra logaritmi, potenze, esponenziali.
Esercizio 69 (§ 4.3).
Esponenziali e logaritmi generali (con base
.
Esercizio 28 (§ 4.3).
Crescita e decadimento delle funzioni esponenziale esponenziale e logaritmo.
Comportamento asintotico e confronto tra logaritmi, potenze, esponenziali.
Esercizio 69 (§ 4.3).
Esponenziali e logaritmi generali (con base ![]() ).
Esercizio 13 (§ 4.3).
).
Esercizio 13 (§ 4.3).
[4.2, 4.3, 4.4]