Università degli Studi di Firenze
Ingegneria per l'Ambiente e il Territorio
Corso di Analisi Matematica I
Periodo: 24 settembre - 11 novembre 2001.
Docente: prof.ssa Francesca Bucci.
I capitoli, le sezioni e le pagine indicate al termine di ogni lezione si
riferiscono al testo di riferimento
(M. Giaquinta e G. Modica, ANALISI MATEMATICA (1.
Funzioni di una variabile), Pitagora Editrice, Bologna, Ristampa 1999).
Senza dimostrazione è abbreviato con s.d., per esercizio con p.e., dimostrato con dim.
1. Mer. 26/9/01 - 2 ore
Presentazione del corso. Libro di testo e altri testi consigliati. Alcune informazioni pratiche.
NUMERI REALI: proprietà algebriche e d'ordine dei numeri reali.
Estremo superiore, estremo inferiore e assioma di continuità.
Numeri interi e numeri razionali. ![]() non è razionale (s.d.).
Principio di Archimede.
Un pò di sintassi (cfr. p. 4); i quantificatori.
[pp. 1-4, 7-10; p. 58].
non è razionale (s.d.).
Principio di Archimede.
Un pò di sintassi (cfr. p. 4); i quantificatori.
[pp. 1-4, 7-10; p. 58].
2. Gio. 27/9/01 - 2 ore
Valore assoluto di un numero reale. Proprietà del valore assoluto: la disuguaglianza triangolare (dim.). La seconda disuguaglianza triangolare (dato p.e.). Intervalli, semirette. Distanza. Alcuni esercizi scelti da 4.1 e 4.7 di pag. 48. [pp. 5, 8-10].
3. Lun. 1/10/01 - 2 ore
Riferimento cartesiano sulla retta, riferimento cartesiano nel piano.
Il concetto di FUNZIONE. Dominio, codominio, immagine di una funzione. Funzioni reali. Grafico di una funzione. Funzioni iniettive, surgettive. Funzioni di variabile reale a valori reali. Esempi (rette, parabola, valore assoluto, parte intera). Funzioni pari e funzioni dispari. Composizione di funzioni. Esempi. [pp. 10-12; 29-34, 39. Consigliata la lettura del § 2.3].
4. Mer. 3/10/01 - 2 ore
Funzione inversa. Grafico dell'inversa. Funzioni (strettamente) crescenti, (strettamente) decrescenti; funzioni monotòne. Parentesi: la terminologia degli insiemi e le operazioni di unione, intersezione, complementare.
FUNZIONI CONTINUE di variabile reale: definizione, esempi. Proposizione su continuità e operazioni di calcolo tra funzioni. Corollario: i polinomi e le funzioni razionali fratte sono continue. Zeri di funzioni continue: introduzione. [pp. 40-41, consigliata la lettura dei §§ 3.4, 3.5; pp. 68, 69, 72; 72-74 (cfr. 54-55)].
5. Gio. 4/10/01 - 2 ore
Esercizio alla lavagna con studente: la funzione ![]() ,
, ![]() ,
è continua in ogni
,
è continua in ogni ![]() .
.
Teorema degli zeri (s.d.). Esempi di non validità del teorema degli zeri.
Alcune conseguenze: esistenza della radice quadrata e della radice ![]() esima
di un numero positivo
esima
di un numero positivo ![]() .
[p. 74; 5-6, 8].
.
[p. 74; 5-6, 8].
6. Lun. 8/10/01 - 2 ore
Alcune conseguenze del teorema degli zeri:
l'immagine di una funzione continua su un intervallo è un intervallo (s.d.);
l'inversa di una funzione continua su un intervallo è continua.
Esempi: continuità di ![]() ,
, ![]() .
.
LIMITI. Limiti finiti: definizione, osservazioni fondamentali ed esempi. La retta reale estesa. Il linguaggio degli intorni. Limiti infiniti e all'infinito. Proprietà del passaggio al limite: unicità, località, etc. [cfr. Cap. II, §2.1 e 2.2: pp. 74-78; 53-60, 64-65].
7. Mer. 10/10/01 - 2 ore
Limiti (segue dalla lezione precedente).
Dal limite alla funzione: Teorema della permanenza del segno (dim.).
Funzioni limitate. Una funzione che ha limite finito per ![]() è localmente limitata intorno a
è localmente limitata intorno a ![]() (dim.).
Funzioni che non hanno limite per
(dim.).
Funzioni che non hanno limite per ![]() :
: ![]() ,
, ![]() .
Il calcolo dei limiti: somma, prodotto, quoziente di funzioni che
hanno limite finito. Il calcolo di limiti infiniti: alcuni esempi.
Analisi di
.
Il calcolo dei limiti: somma, prodotto, quoziente di funzioni che
hanno limite finito. Il calcolo di limiti infiniti: alcuni esempi.
Analisi di
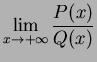 ,
con
,
con ![]() ,
, ![]() polinomi.
Continuità della funzione
polinomi.
Continuità della funzione ![]() ed introduzione della funzione
inversa
ed introduzione della funzione
inversa ![]() .
[pp. 61-63, 64-70; 79].
.
[pp. 61-63, 64-70; 79].
8. Gio. 11/10/01 - 2 ore
Proprietà dell'operazione di passaggio al limite (segue dalla lezione
precedente):
criterio del confronto, limiti di funzioni monotone.
Esercizi con i limiti (esempi del tipo
![]() ,
, ![]() ).
).
La nozione di DERIVATA. Le funzioni derivabili sono continue (dim.).
Significato geometrico: la retta tangente. Esempi di funzioni non derivabili
in ![]() :
: ![]() ,
, ![]() .
[pp. 63-64; Cap. III: § 1.1, 1.2 fino a p. 93].
.
[pp. 63-64; Cap. III: § 1.1, 1.2 fino a p. 93].
9. Lun. 15/10/01 - 2 ore
Derivate di funzioni elementari (![]() ,
, ![]() ).
Regole di derivazione: derivate di somme, prodotti, rapporti;
derivazione di funzioni composte, derivata della funzione inversa
(giustificazione della formula per via geometrica).
Derivate successive.
[Cap. IV: §§ 1.1, 1.2, 1.3].
).
Regole di derivazione: derivate di somme, prodotti, rapporti;
derivazione di funzioni composte, derivata della funzione inversa
(giustificazione della formula per via geometrica).
Derivate successive.
[Cap. IV: §§ 1.1, 1.2, 1.3].
10. Mer. 17/10/01 - 2 ore
ESTREMI di funzioni reali di una variabile reale. Punti di massimo o minimo relativo: definizione ed esempi. Teorema di Fermat (dim.). Punti critici. Teorema di Weierstrass (s.d.). Teorema di Lagrange (s.d.). Test di monotonia per le funzioni derivabili (dim.). Problemi di minimo: il problema del calorimetro. [Cap. II: § 2.3; Cap. III: § 1.4].
11. Gio. 18/10/01 - 2 ore
Funzioni di classe ![]() . Condizioni del second'ordine per l'esistenza di
punti di estremo relativo: condizioni sufficienti e condizioni
necessarie (dim.). Esempi e controesempi.
. Condizioni del second'ordine per l'esistenza di
punti di estremo relativo: condizioni sufficienti e condizioni
necessarie (dim.). Esempi e controesempi.
Grafici di funzioni. Esercizi su: derivazione di funzioni composte, grafici di funzioni e problemi di minimo. [Cap. V: § 5].
12. Lun. 22/10/01 - 2 ore
Funzioni con derivata nulla su un intervallo.
La nozione di INTEGRALE di una funzione. Funzioni integrabili secondo Riemann e integrale. Proprietà della classe delle funzioni integrabili. L'integrale è monotono e lineare. Diseguaglianza del modulo. Alcune classi di funzioni integrabili (s.d). [Cap. III: § 1.4, Prop. 1.18 e Oss. 1.19. § 2.1, §2.2.].
13. Mer. 24/10/01 - 2 ore
Funzioni integrali. Funzioni Lipschitziane. Teorema fondamentale del calcolo integrale (dim.). La funzione integrale come primitiva. Teorema della media.
Funzione logaritmo: definizione (come funzione integrale) e proprietà. [Cap. III: sez. 3; consigliata la lettura della sez. 4. Cap. IV: §§ 6.2, 6.3].
14. Gio. 25/10/01 - 2 ore
Funzione esponenziale: definizione (come l'inversa del logaritmo)
e proprietà.
Logaritmo in base ![]() (
(![]() ,
, ![]() ) e la funzione inversa
) e la funzione inversa ![]() .
Potenze ad esponente reale
.
Potenze ad esponente reale ![]() :
: ![]() ,
, ![]() .
.
PRIMITIVE. Applicazioni del teorema fondamentale del calcolo. Esempi ed alcuni esercizi. [Cap. IV: § 6.3. Esercizi 8.44, 8.50]
15. Lun. 29/10/01 - 2 ore
Funzioni logaritmo, esponenziale, potenza: proprietà fondamentali e grafici.
Prime equazioni differenziali: ![]() , equazione differenziale
della crescita (
, equazione differenziale
della crescita (![]() ) e del decadimento (
) e del decadimento (![]() ).
Soluzione dell'equazione.
).
Soluzione dell'equazione.
Funzioni trigonometriche. La funzione arcotangente: definizione e proprietà. La funzione tangente (come funzione inversa dell'arcotangente). Funzioni seno e coseno. [Cap. IV: selezionare da § 2 e § 6].
16. Mer. 31/10/01 - 2 ore
Le funzioni arcoseno e arcocoseno, definizione e loro derivate (derivazione della funzione inversa).
Integrali indefiniti. Metodi di integrazione: integrazione per parti e per sostituzione. Esempi ed esercizi. [Cap. IV: § 5]
17. Lun. 5/11/01 - 2 ore
Tabella di integrali indefiniti.
Applicazione dell'integrazione per parti: gli integrali
![]() ,
,
![]() .
Integrazione di funzioni razionali: richiami sulla divisione di polinomi,
caso di denominatori di grado al più due (riducibili e irriducibili),
denominatori con radici reali di molteplicità maggiore di uno. Esempi.
Sostituzioni razionalizzanti (
.
Integrazione di funzioni razionali: richiami sulla divisione di polinomi,
caso di denominatori di grado al più due (riducibili e irriducibili),
denominatori con radici reali di molteplicità maggiore di uno. Esempi.
Sostituzioni razionalizzanti (![]() ,
, ![]() ). Esempi.
[Cap. IV: sez. 5.2 (esclusi esempi 5.23, 5.27 e 5.28)]
). Esempi.
[Cap. IV: sez. 5.2 (esclusi esempi 5.23, 5.27 e 5.28)]
18. Mer. 7/11/01 - 3 ore
Le funzioni iperboliche ![]() e
e ![]() : definizione, grafici
e loro inverse.
Gli integrali
: definizione, grafici
e loro inverse.
Gli integrali
![]() ,
,
![]() ,
,
![]() : sostituzioni
: sostituzioni
![]() ,
, ![]() ,
, ![]() .
.
Limiti noteveli (forme ![]() , come limiti di rapporti incrementali).
I Teoremi di de l'Hôpital (s.d.). Limiti notevoli (forme
, come limiti di rapporti incrementali).
I Teoremi di de l'Hôpital (s.d.). Limiti notevoli (forme ![]() ,
confronto tra logaritmi, potenze, esponenziali).
[Cap. IV: § 5: esempi 5.27, 5.28; § 6: 6.4.
Cap. V: § 3: sez. 3.1, 3.2.]
,
confronto tra logaritmi, potenze, esponenziali).
[Cap. IV: § 5: esempi 5.27, 5.28; § 6: 6.4.
Cap. V: § 3: sez. 3.1, 3.2.]
19. Gio. 8/11/01 - 2 ore
Alcune disuguaglianze fondamentali relative alle funzioni esponenziali e trigonometriche (Cap. V, sez. 4, 4.1 e 4.2).
Studi di funzione (Cap. V, sez. 5). Studio del segno della derivata prima. Asintoti (orizzontali, verticali, obliqui): esempi. Funzioni periodiche. Funzioni derivabili convesse/concave (Cap. IV, sez. 4, Prop. 4.2 (s.d.)).
Formula di Taylor con resto integrale per funzioni di classe ![]() (Cap. V, introduzione alla sez. 1).
(Cap. V, introduzione alla sez. 1).