Anno Accademico 2001-2002

Università degli Studi di Firenze

Ingegneria per l'Ambiente e il Territorio

Corso di Analisi Matematica II

Periodo: 26 novembre 2001 - 25 gennaio 2002.

Docente: prof.ssa Francesca Bucci.

Lezioni svolte

I capitoli e le sezioni indicate al termine delle lezioni si riferiscono al testo

• M. Bramanti, C.D. Pagani, S. Salsa, MATEMATICA, Zanichelli Editore, 2000

ad eccezione delle lezioni $1$, $2$ e $3$, per le quali si fa riferimento al testo (adottato nel primo periodo)

• M. Giaquinta e G. Modica, ANALISI MATEMATICA (1. Funzioni di una variabile), Pitagora Editrice, Bologna, Ristampa 1999).

Senza dimostrazione è abbreviato con s.d., per esercizio con p.e., dimostrato con dim.

1. Lun. 26/11/01 - 2 ore

Breve presentazione del corso. Libro di testo e altri testi consigliati.

(Continuazione del calcolo differenziale e integrale per funzioni di una variabile) Formula di Taylor con resto integrale (dim. la formula di ordine due), formula di Taylor con resto di Lagrange. Le notazioni di Landau: $f=o(g)$, $f=O(g)$, $f\sim g$. Polinomi di Taylor delle funzioni $e^x$, $\sin x$, $\cos x$.

[Cap. V, sez. 1.1]

2. Mer. 28/11/01 - 1 ora

Formula di Taylor con resto di Peano. Esercizi: applicazioni della formula di Taylor con resto di Peano al calcolo di limiti.

[Cap.V, sez. 1.2]

3. Gio. 29/11/01 - 2 ore

Esercizio: confronto sull'uso della formula di Taylor e del teorema di de L'Hôpital per il calcolo di limiti.

Alcuni sviluppi ottenuti da quello della funzione $\frac1{1-x}$. Sviluppi di Taylor di funzioni elementari. Applicazioni: uso della formula di Taylor con resto integrale per l'approssimazione di numeri. Determinazione di valori approssimati di $e$ e $\pi$ e stima dell'errore.

4. Lun. 3/12/01 - 2 ore

Integrali generalizzati. Il caso di funzioni limitate su insiemi non limitati e il caso di funzioni illimitate su intervalli limitati. Analisi dell'integrabilità in senso generalizzato della funzione $\frac1{x^\alpha}$ su $(1,+\infty)$ e su $(0,1)$, al variare di $\alpha$. Criteri del confronto. Alcuni esempi ( $\int_0^\infty\, e^{-x^2}\,dx$, $\int_0^\infty \cos (x^2)\,dx$, ...). La funzione Gamma di Eulero.

[Cap. 6, sez. 6.2, 6.3, 6.4.]

5. Mer. 5/12/01 - 1 ora

Esercizi su integrali generalizzati.

6. Gio. 6/12/01 - 2 ore

Esercizio: studio della funzione

$$F(x) = \int_0^{x^2} \frac1{\sqrt{1-t^2}}\,dt\,.$$

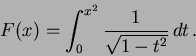
Equazioni Differenziali Ordinarie (EDO). Equazioni del primo ordine: definizione di soluzione. L'equazione lineare $y' = a(t)y + b(t)$, con $a$, $b\in C^0(I)$, $I\subseteq \mathbb{R}$: determinazione dell'integrale generale, problema di Cauchy associato e unicità della soluzione corrispondente.

[Cap. 7, sez. 1-2]

7. Lun. 10/12/01 - 2 ore

Esercizi su equazioni lineari del I ordine.

Un primo esempio di equazione del secondo ordine: l'equazione dell'oscillatore armonico $y'' + \omega^2 y = 0$, $\omega\ne 0$. Determinazione dell'unica soluzione del problema di Cauchy associato.

8. Mer. 12/12/01 - 1 ora

EDO del secondo ordine: definizione di soluzione. EDO lineari del secondo ordine. (i) L'equazione omogenea: soluzioni linearmente indipendenti, matrice wronskiana e criterio del determinante wronskiano, struttura dell'integrale generale. (ii) Struttura dell'integrale generale dell'equazione completa.

[Cap. 7, sez. 3.1]

9. Gio. 13/12/01 - 2 ore

Numeri complessi ed esponenziali complessi. Rappresentazione geometrica dei numeri complessi: il piano di Gauss. Forma trigonometrica di un numero complesso: modulo, argomento, argomento principale. Operazioni di prodotto, divisione, elevamento a potenza: formula di de Moivre. Definizione dell'esponenziale $e^{i\theta}$, $\theta\in \mathbb{R}$, definizione dell'esponenziale complesso $e^z$, $z\in \mathbb{C}$; proprietà del calcolo.

EDO lineari del secondo ordine a coefficienti costanti. Analisi dell'equazione omogenea $y'' + a y' + by =0$: l'equazione caratteristica. Determinazione dell'integrale generale come combinazione lineare di soluzioni linearmente indipendenti.

[Cap. 1, sez. 8.3; Cap. 5, sez. 6.2; Cap. 7, sez. 3.2]

10. Lun. 17/12/01 - 2 ore

EDO lineari del secondo ordine: l'equazione non omogenea $y'' + a y' + by = f(t)$, $a$, $b$ costanti, $f\in C^0(I)$, $I\subset \mathbb{R}$. Ricerca di un integrale particolare nel caso in cui $f(t) = P_n(t) e^{\lambda t}$, $P_n(t)$ polinomio di grado $n$. Metodo dei coefficienti indeterminati: esempi ed esercizi.

[Cap. 7, sez. 3.3]

11. Mer. 19/12/01 - 1 ora

EDO lineari non omogenee: il metodo di variazione delle costanti. Esempi.

[Cap. 7, sez. 3.3]

12. Gio. 20/12/01 - 2 ore

EDO del I ordine: il problema dell'unicità della soluzione del problema di Cauchy. Esempio di non unicità. Soluzioni locali e globali. Esempio di blow up (scoppiamento in tempo finito).

EDO a variabili separabili. Esempi. Cenni allo studio qualitativo di EDO.

[Cap. 7, sez. 2.1, 2.2]

Lun. 7/1/02

Lezione sospesa per malattia della docente.

13. Mer. 9/1/02 - 2 ore

Funzioni reali di più variabili reali. Gli intorni in $\mathbb{R}^n$, $n>1$. Insiemi limitati. Punti interni, esterni, di frontiera. Insiemi aperti e chiusi, regioni di $\mathbb{R}^2$. Esempi.

Limiti di funzioni di più variabili. Esempi. Funzioni continue. Il teorema di Weierstrass (s.d.).

[Cap. 11, § 1]

14. Gio. 10/1/02 - 2 ore

Derivate parziali. Esempi. Il vettore gradiente. Differenziabilità e approssimazione lineare.

[Cap. 11, sez. 2.1]

15. Lun. 14/1/02 - 2 ore

Funzioni differenziabili: piano tangente al grafico. Proprietà delle funzioni differenziabili: $f$ differenziabile in $(x_0,y_0)$ implica (i) $f$ continua in $(x_0,y_0)$; (ii) $f$ ammette derivate parziali in $(x_0,y_0)$; (iii) esiste il piano tangente al grafico di $f$ nel punto $(x_0,y_0,f(x_0,y_0))$. Il Teorema del differenziale totale (s.d.). Corollario: $f\in C^1(A)$, $A$ aperto di $\mathbb{R}^2$, implica $f$ differenziabile in $A$. Il differenziale. Esempi ed esercizi.

[Cap. 11, sez. 2.2, 2.3]

16. Mer. 16/1/02 - 1 ora

Derivate direzionali. Esempi. Funzioni differenziabili: formula per il calcolo delle derivate direzionali (dim.). Derivazione di funzioni composte: la regola della catena (s.d.).

[Cap. 11, sez. 2.4, 2.5]

17. Gio. 17/1/02 - 2 ore

Esercizi su derivate parziali, differenziali, piani tangenti, derivate direzionali, derivazione di funzioni composte.

18. Lun. 21/1/02 - 2 ore

(Continuazione di) Derivate direzionali: direzioni di massima e minima crescita.

Derivate di ordine superiore. Il teorema di Schwarz (s.d.). Funzioni di classe $C^2$. Matrice hessiana. Esempio: l'operatore di Laplace (o laplaciano) $\Delta: f\rightarrow \sum_{i=1}^n \frac{\partial^2 f}{\partial x_i^2}$, l'equazione di Laplace $\Delta f=0$. Applicazione della derivazione di funzioni composte: l'equazione di Laplace in coordinate polari.

[Cap. 11, sez. 3.1]

19. Mer. 23/1/02 - 1 ora

Applicazioni delle derivate parziali: punti di estremo relativo per funzioni di più variabili. Il Teorema di Fermat (dim.): Sia $f: A\subset \mathbb{R}^n \to \mathbb{R}$ e sia $x_0$ un punto di estremo relativo per $f$ interno ad $A$. Se $f$ è differenziabile in $x_0$, allora $\nabla f(x_0)=0$. Punti critici (o stazionari); punti di sella. Vari esempi.

[Cap. 11, sez. 4.1]

20. Gio. 24/1/02 - 2 ore

Formula di Taylor di ordine due, con resto di Lagrange (dim.) e con resto di Peano (s.d.), per funzioni $f\in C^2(A)$, $A$ aperto di $\mathbb{R}^2$. Classificazione dei punti critici nel caso di funzioni di due variabili: criterio con la matrice hessiana (Teorema 4.7, pag. 401). Esempi ed esercizi.

[Cap. 11, sez. 3.2, 4.2, 4.3]